机器学习----神经网络
机器学习----神经网络
概念合集（写得较为复杂）
机器学习（2）——线性回归（Linear Regression） - 知乎
机器学习（3）——Logistic回归（Logistic Regression） - 知乎
机器学习（5）——神经网络（Neural Network，NN） - 知乎
通俗易懂（合集）：从函数到神经网络
进阶，概念，下饭（漫士沉思录）90分钟！清华博士带你一口气搞懂人工智能和神经网络
（3Blue1Brown）【官方双语】深度学习之神经网络的结构 Part 1 ver 2.0
机器学习的基本流程（从函数到神经网络）
机器学习是要找一个函数，对于给定的输入能给出正确的输出。例如聊天机器人就是输入当前的对话场景，输出机器的应答；语音识别就是输入待辨识的音频，输出对应的文字。
函数（function）
Functions Describe the World ----不是我说的
这个Functions完美的符合了所有点，解释了整个World，这即是早期人工智能符号主义，使用准确的函数准确描述所有结果。
但是现实世界中许多问题无法使用准确的函数描述，只能简化问题，核心思想就是“猜”和“差不多得了”。这即是现代联结主义，希望通过对大脑生理结构复杂性模拟来实现智能。
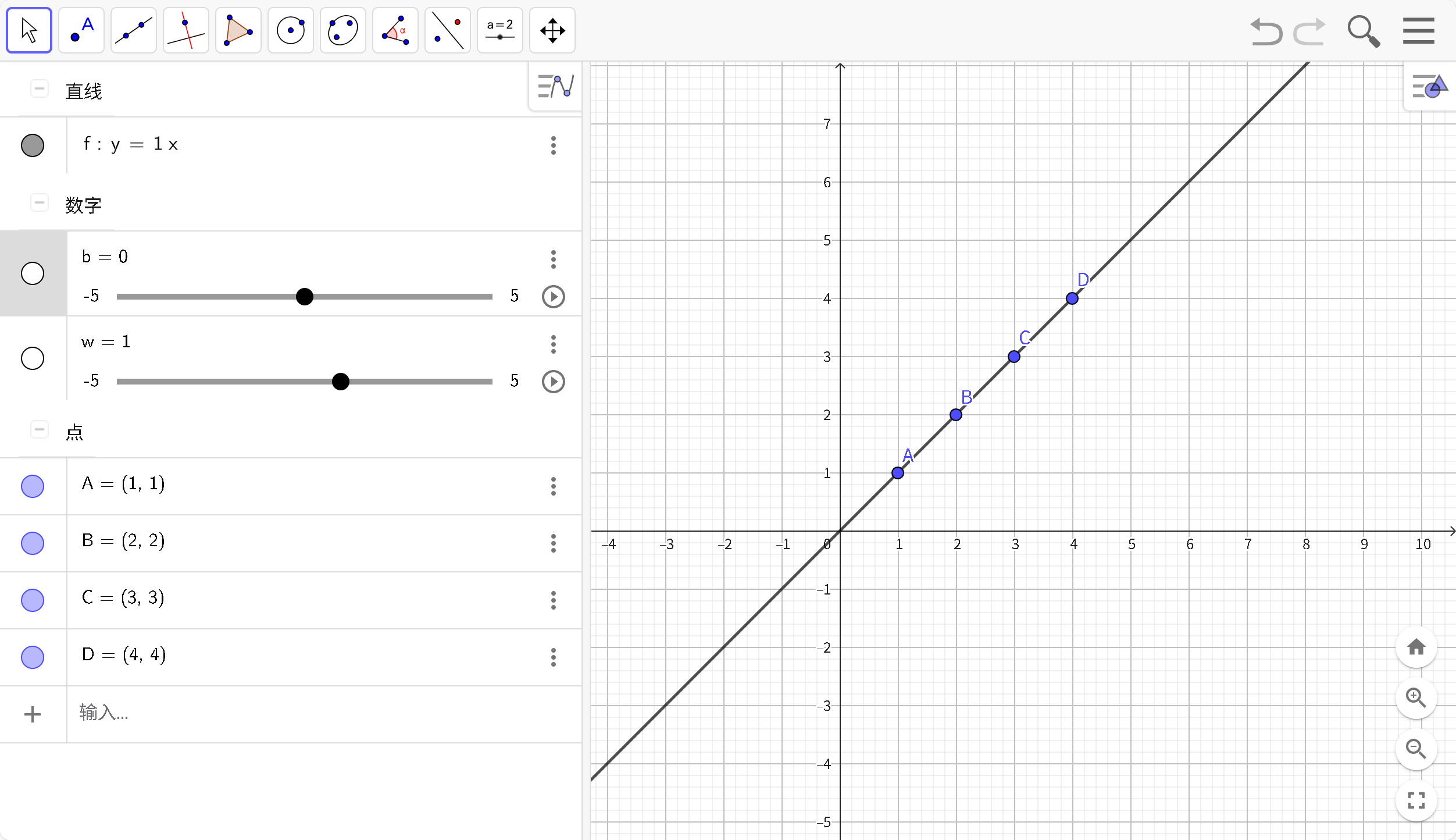
我们首先提供给机器一个特定的函数 f0 （建模），让机器评价它的好坏， 并对它不断进行改进（其过程即是不断的猜），期望最终得到一个最佳的函数 f∗ .
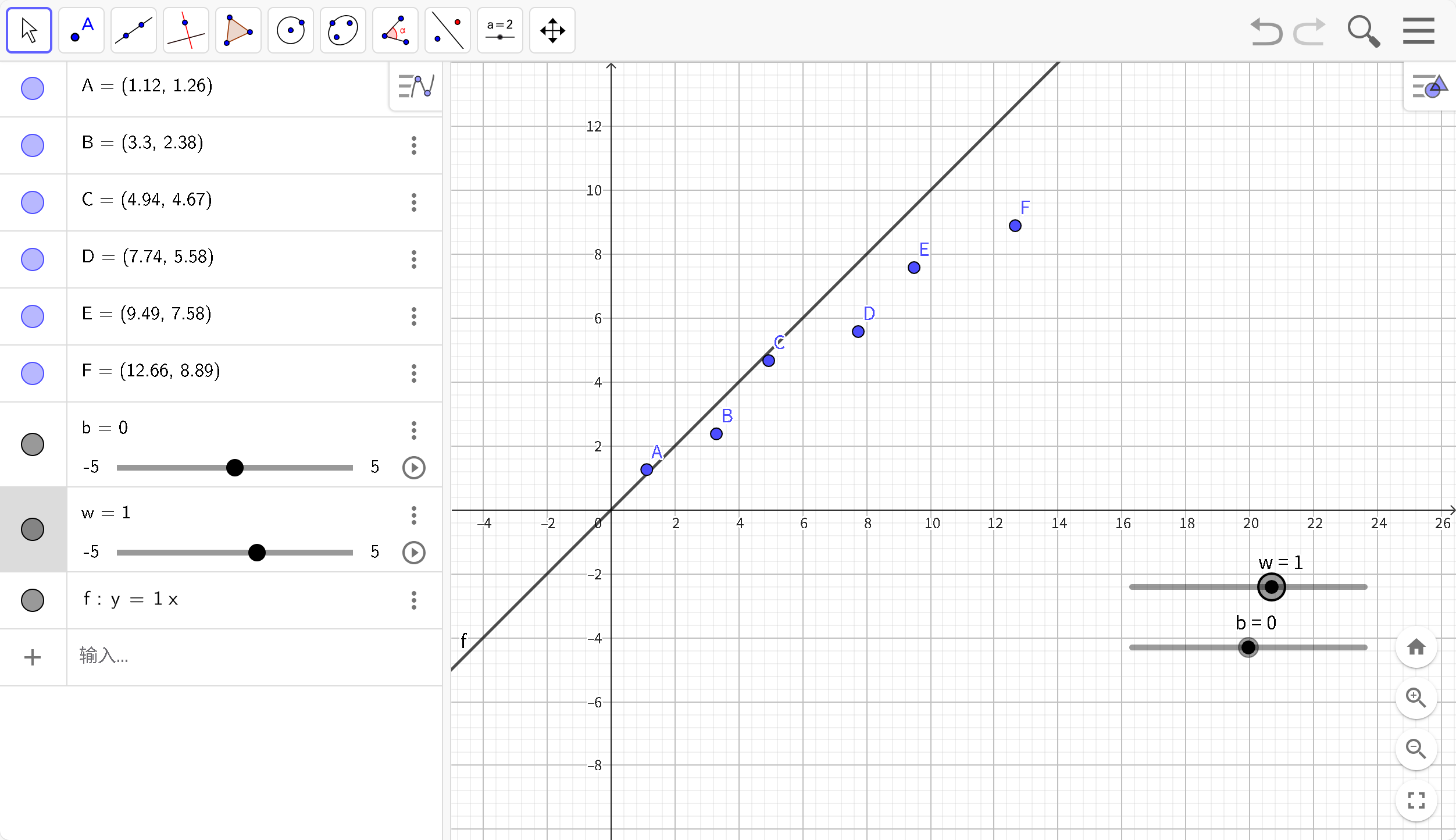
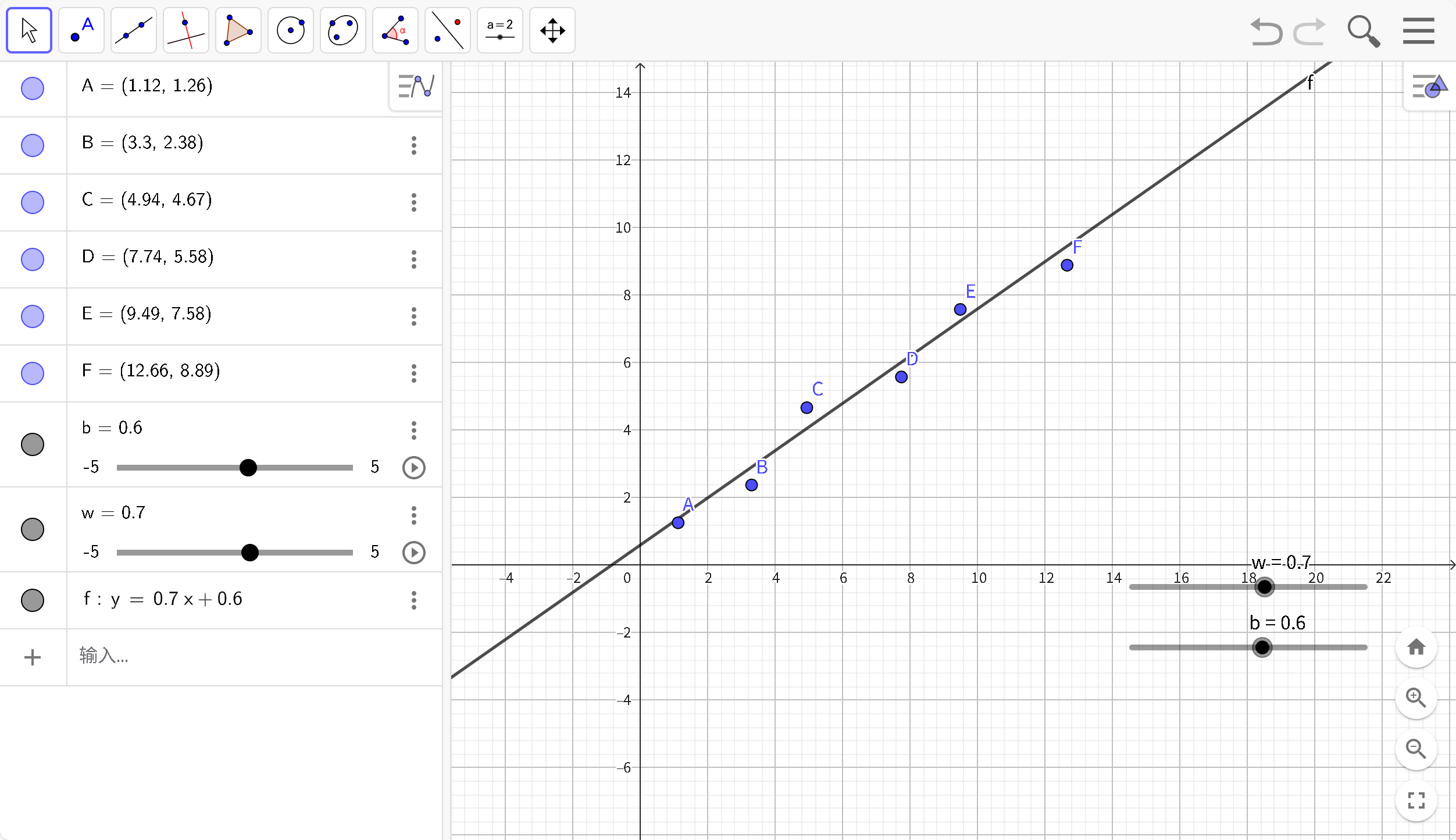
在这个简单的示例中，使用一次函数(模型：Y= wX + b)尽可能接近所有点，但是始终无法通过所有点，那就使用差不多得了，认为现在得到w,b就是最优解。
激活函数（Activation Function）
但是，大多数实际数据并非线性关系，为了简单的将原来的线性函数（Y= wX + b）转化为非线性，可以在原本的函数外层套上一个非线性运算，叫激活函数
F(x) = wX + b ==> F(x) = g(wX + b)
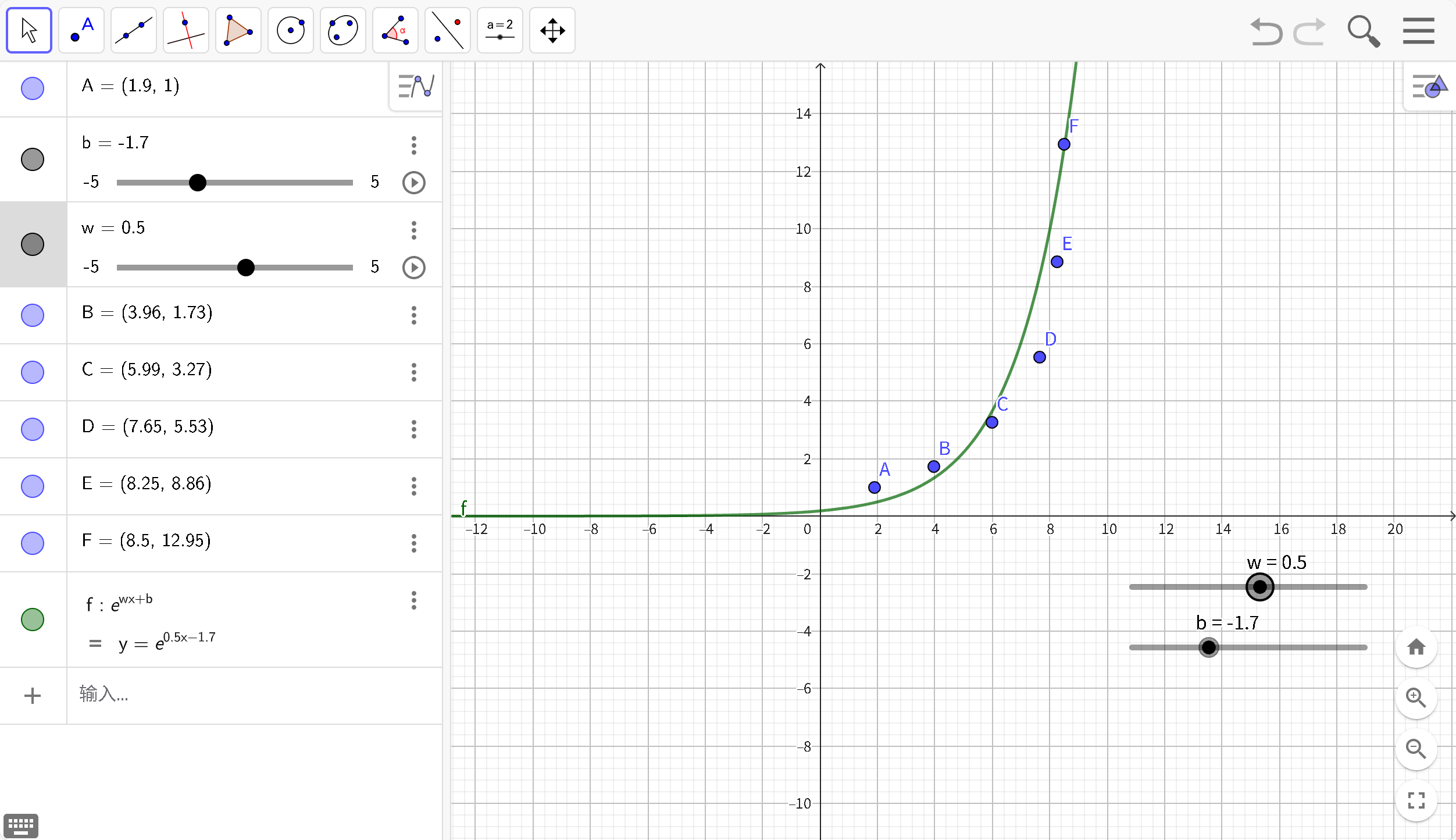
现在，通过添加激活函数g(x)=ex，能够较好的处理非线性数据关系，实际的激活函数比举例的要复杂一点点。
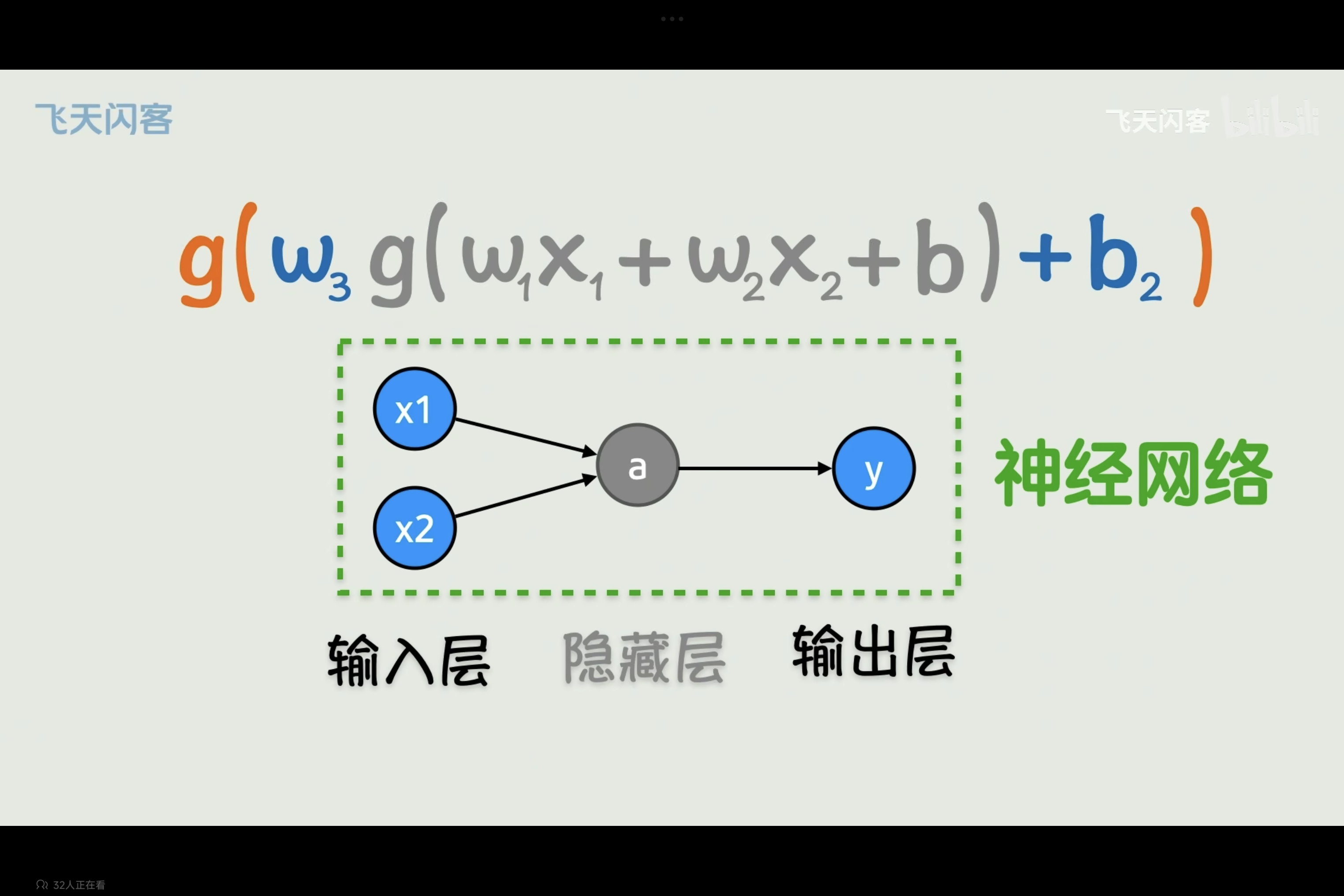
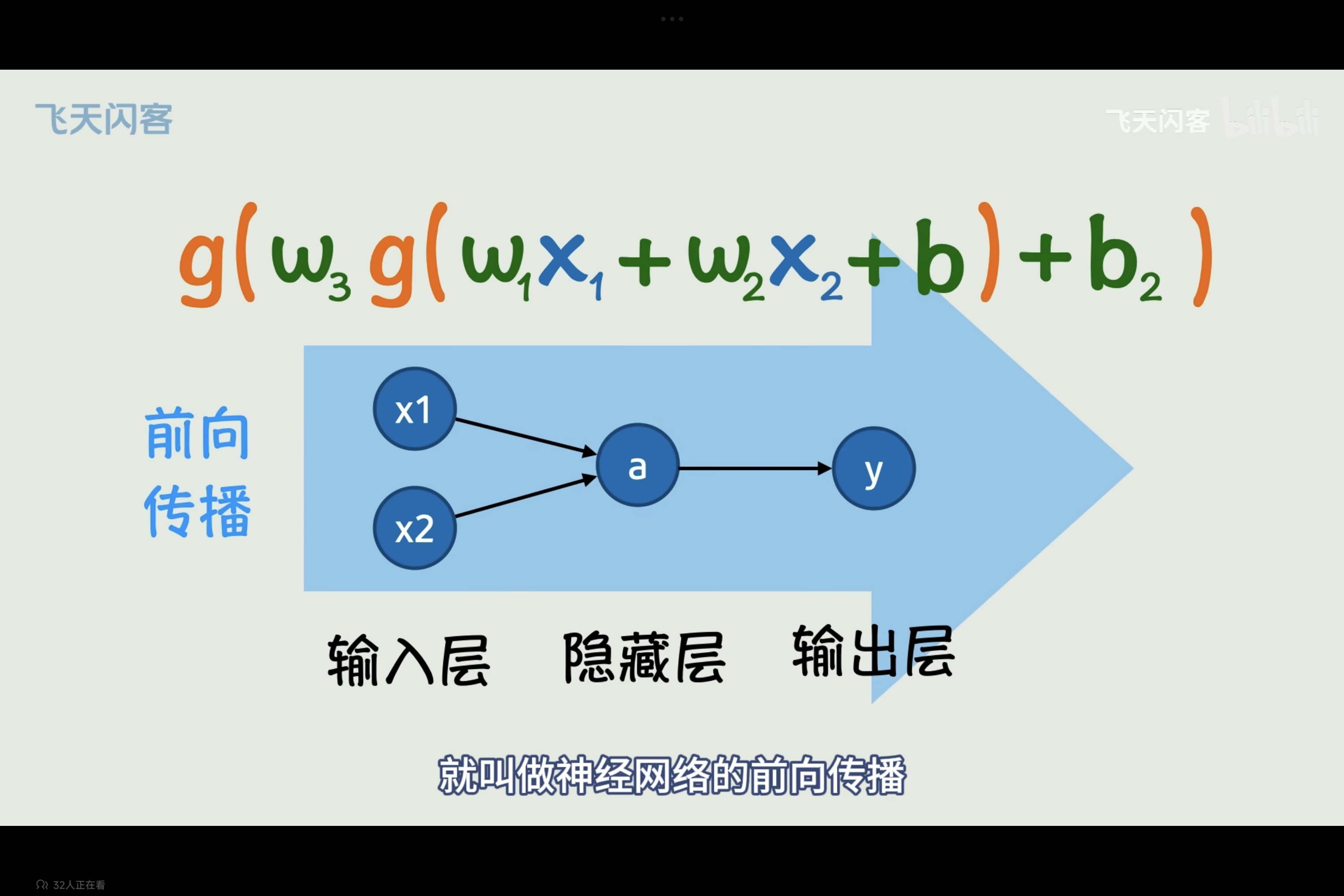
概念：将原本的复杂F(x)画成图的形状，类似神经元的连接（不要理解为真正生物神经突触连接）叫神经网络，神经元连接过程即为一个函数计算过程。
概念及其简单，不要因为名词陌生而觉得过于高端，理解过后既是及其简单的定义。
输入层：即函数输入。
隐藏层：因为套用多层激活函数，位于中间隐藏起来的层。
输出层：即完成函数计算输出结果。
前向传播：即按照神经网络依次正向计算得到结果的过程。
评估----损失函数（lossfunction）
建模、评价和改进，就是机器学习最基本的三个步骤。 ----不是我说的
建模已经完成，能够完成猜的过程，但是，怎样才能评判猜得好不好呢，那就得指定一个标准来评判谁猜得更好，其依据即为损失函数
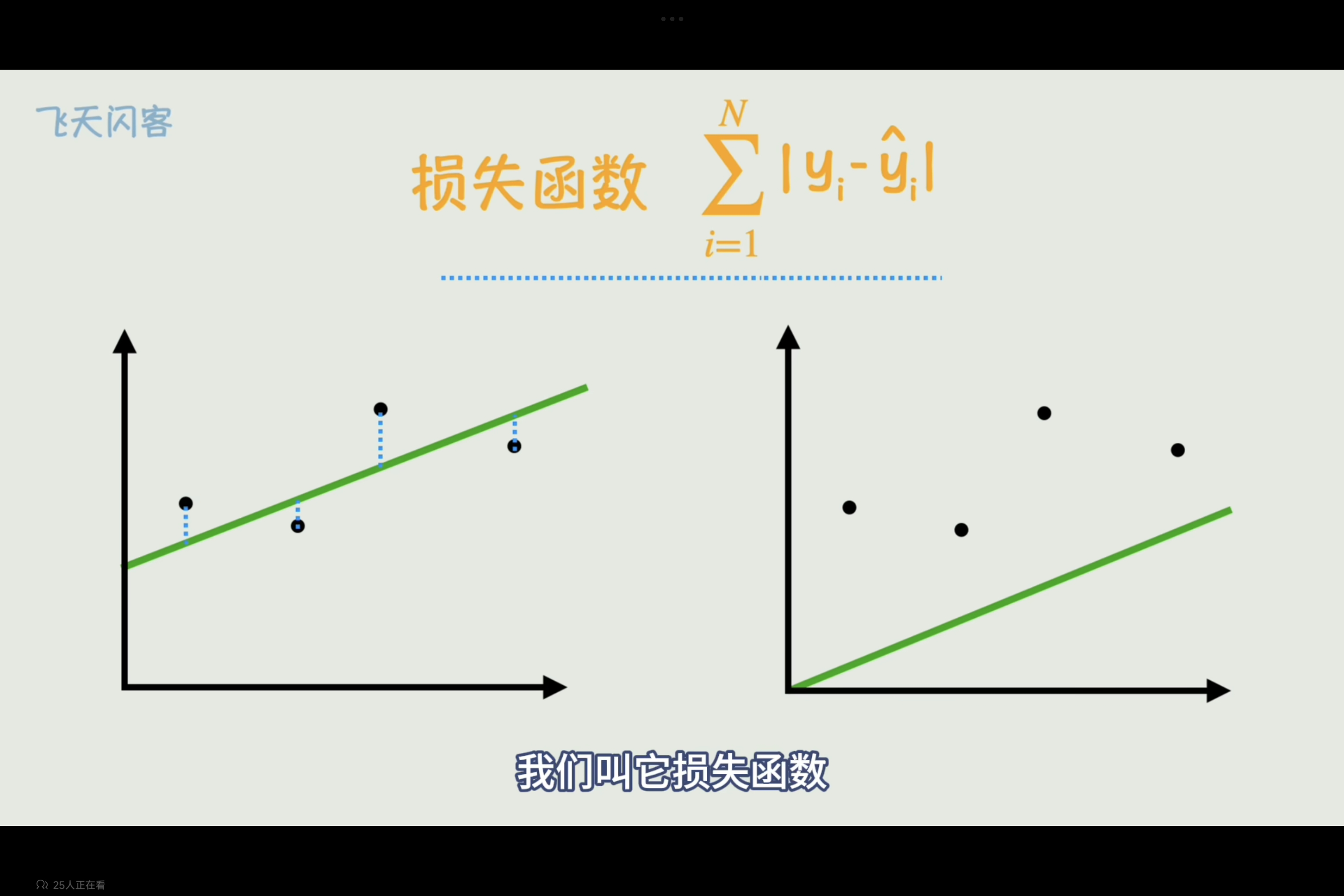
损失函数表示的是真实值与预测值的误差，在不断猜的过程中就是调整w,b的值使损失函数最小的优化问题，简单的函数可以求导为0求极值点来找到，而有w,b两个变量即是求各自的偏导。
以上通过线性函数来拟合x,y之间的关系即为线性回归
神经网络的损失函数
线性回归的损失函数一般可以通过求导或求偏导的方式获取其极值点，但是，神经网络通常由线性函数和非线性激活函数多种复杂组合而成，其损失函数也应当是复杂的非线性函数，但是解决的办法却没有那么复杂，只需要一点点猜即可，通过不断的调整w,b再计算损失函数，观察损失函数的变化，是增加还是减小，能得到当前调整的参数对结果的影响，尽可能将损失函数结果变小。
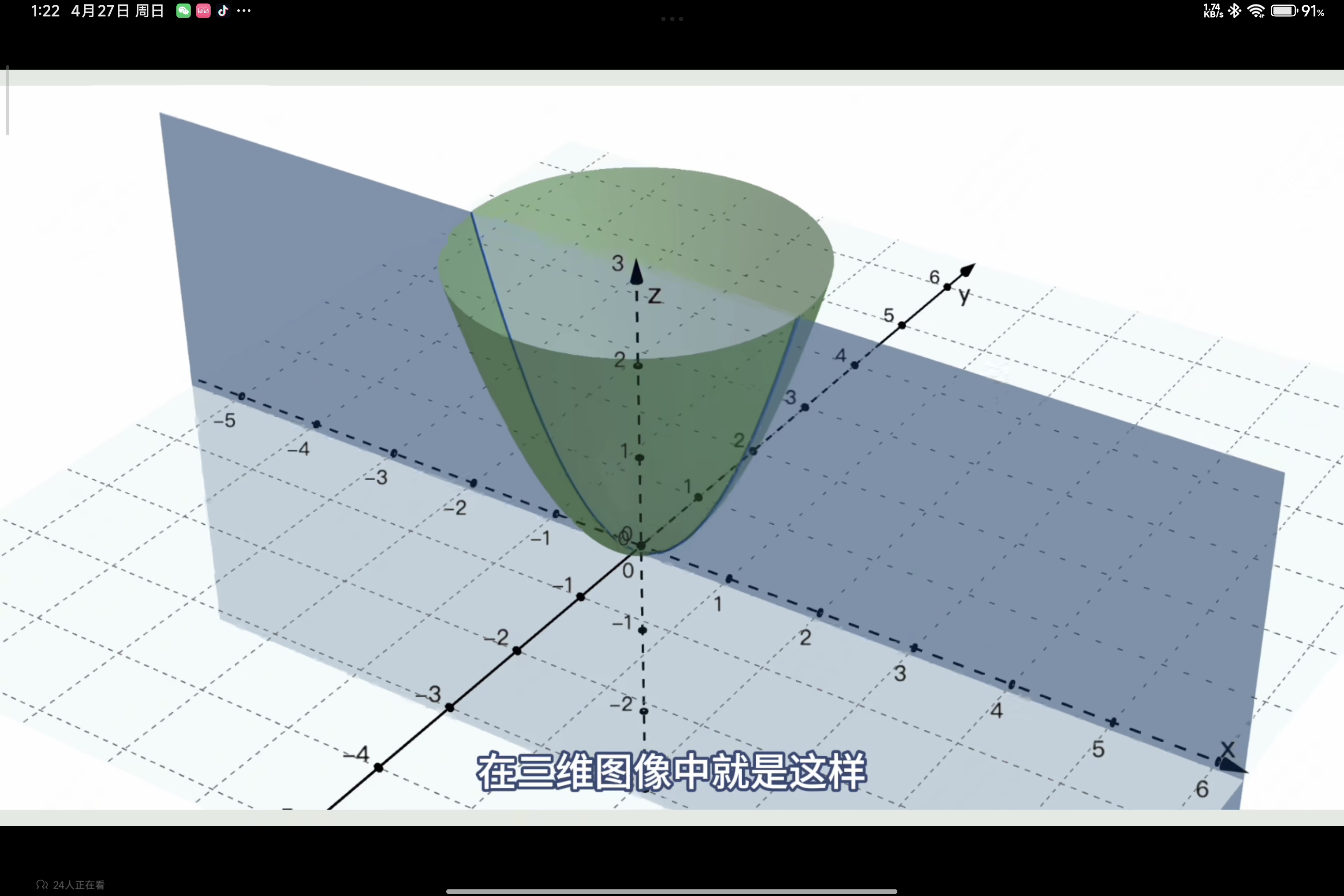
w变化的大小使得损失函数变化的大小即为损失函数对w的偏导，每次只需要让参数向偏导的反方向变化
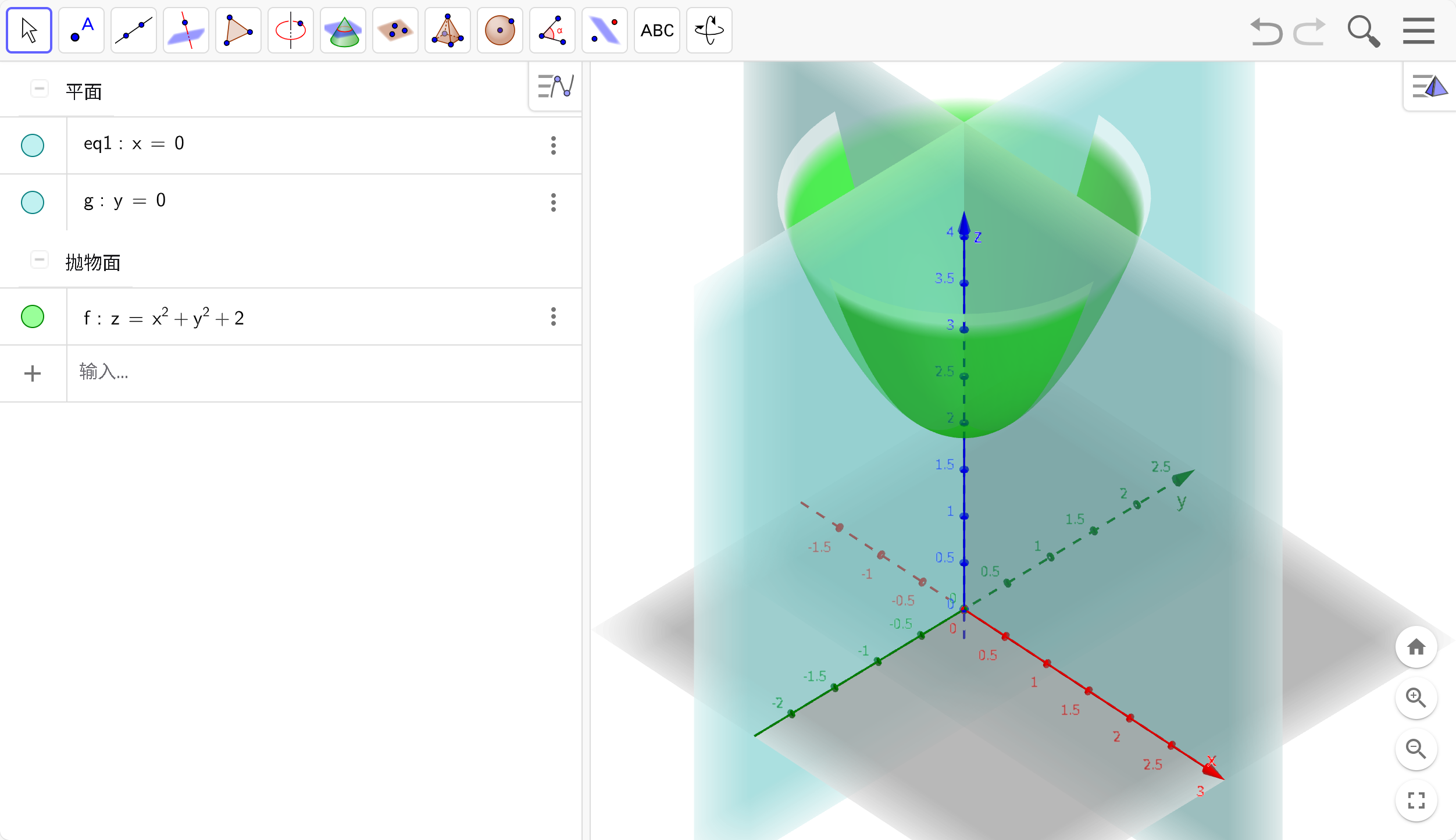
如图，函数最低点位于（0，0，2）其变量为x,y，在y=0平面上，不断尝试向损失函数关于x的偏导的反方向调整，即可到达最低点。
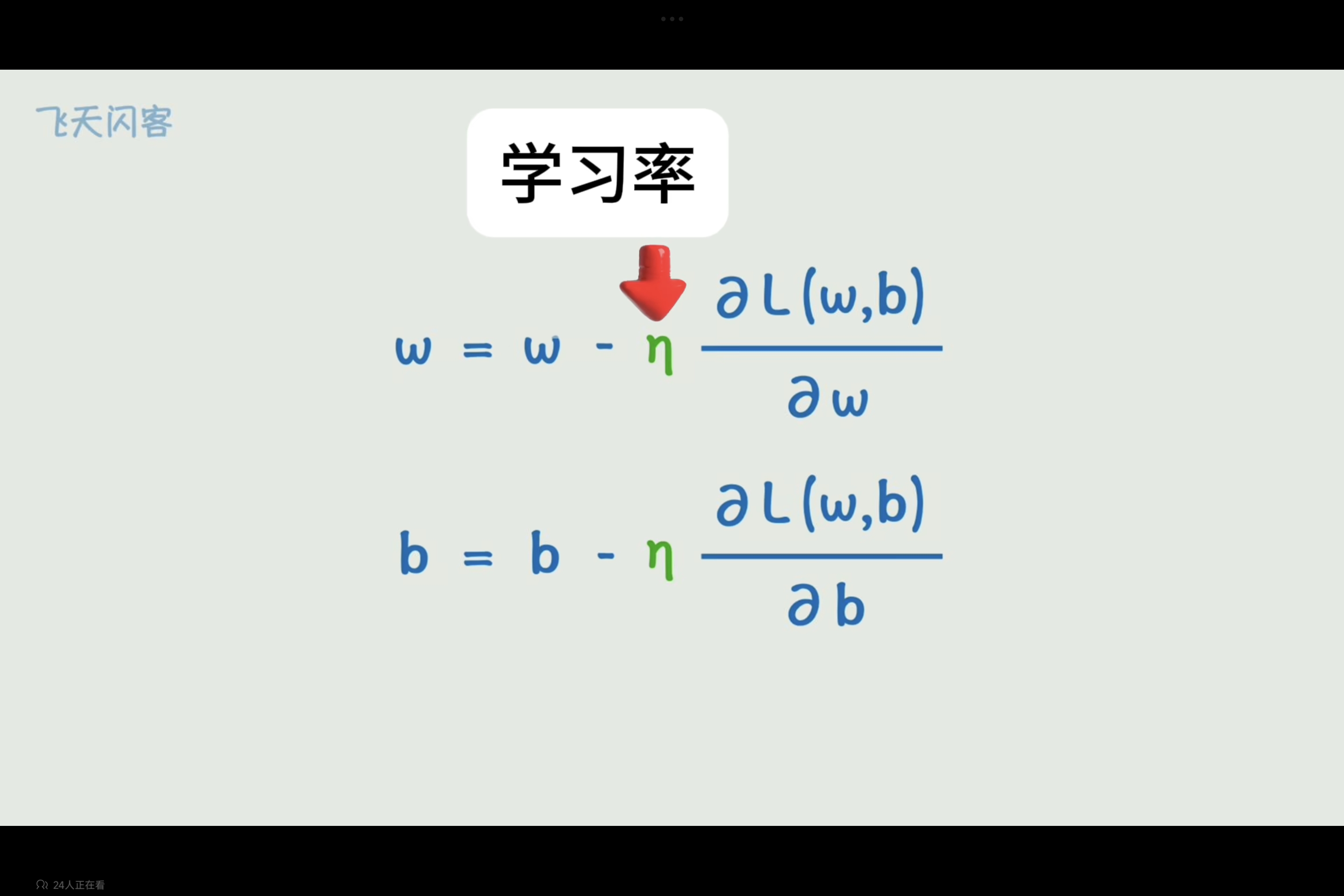
而控制变化快慢的系数即为学习率。
这些偏导数构成的向量就叫梯度。
不断变化w,d参数，使损失函数逐渐变小的过程就叫梯度下降。
反向传播
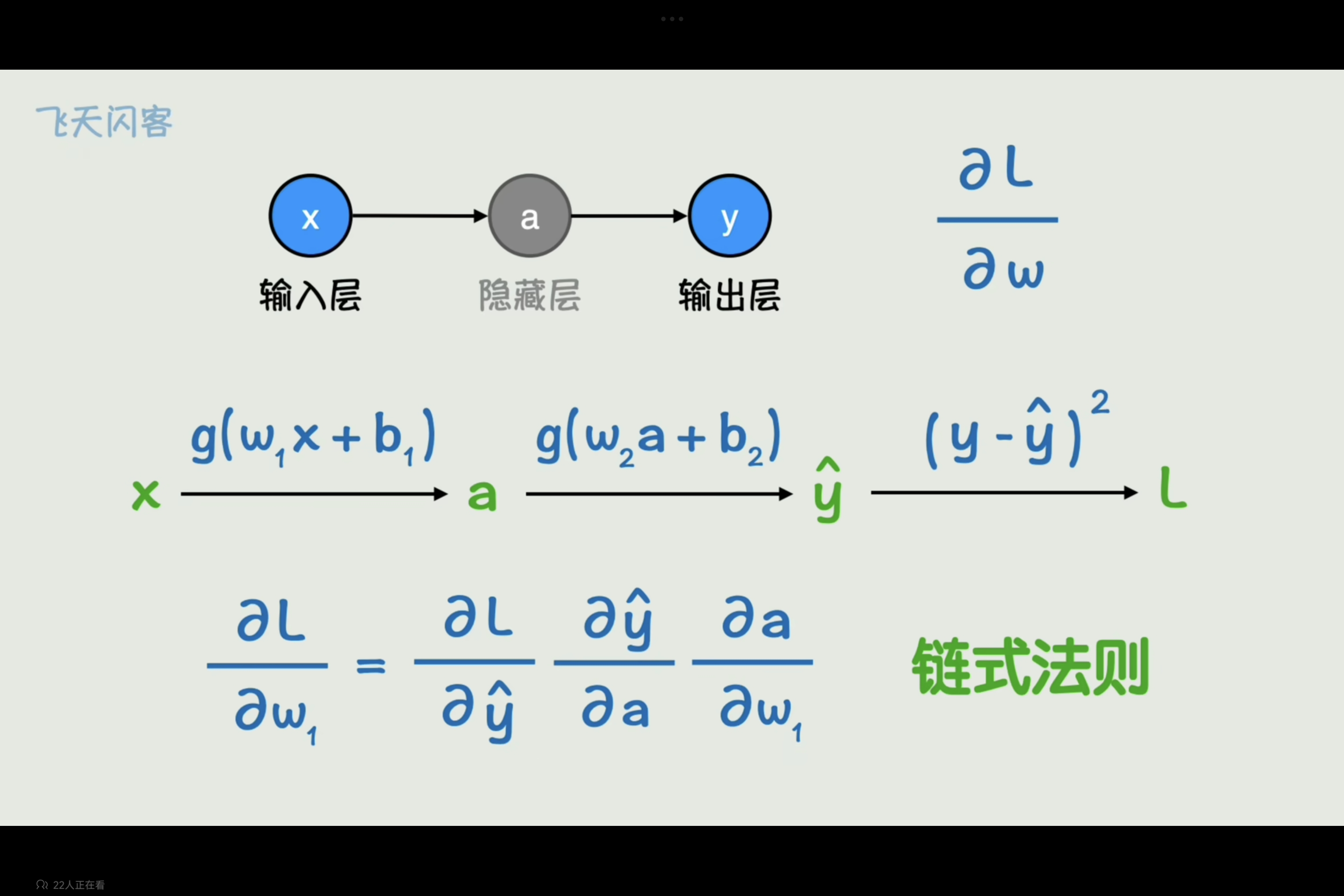
神经网络中求参数对损失函数偏导可以使用链式法则，即损失函数对w1的偏导为“w1变化一个单位使得a变化多少，a变化一个单位使得^y变化多少，^y变化一个单位使得L变化多少，将三者偏导乘在一起，即得到偏导。
然后从右向左依次求导，然后更新每一层参数，例如计算完^y对w2的偏导（a隐藏层的参数w2，b2），在计算损失函数对w1的偏导时也会用到，即可不用重复计算，而是让值从右向左传播，叫反向传播。
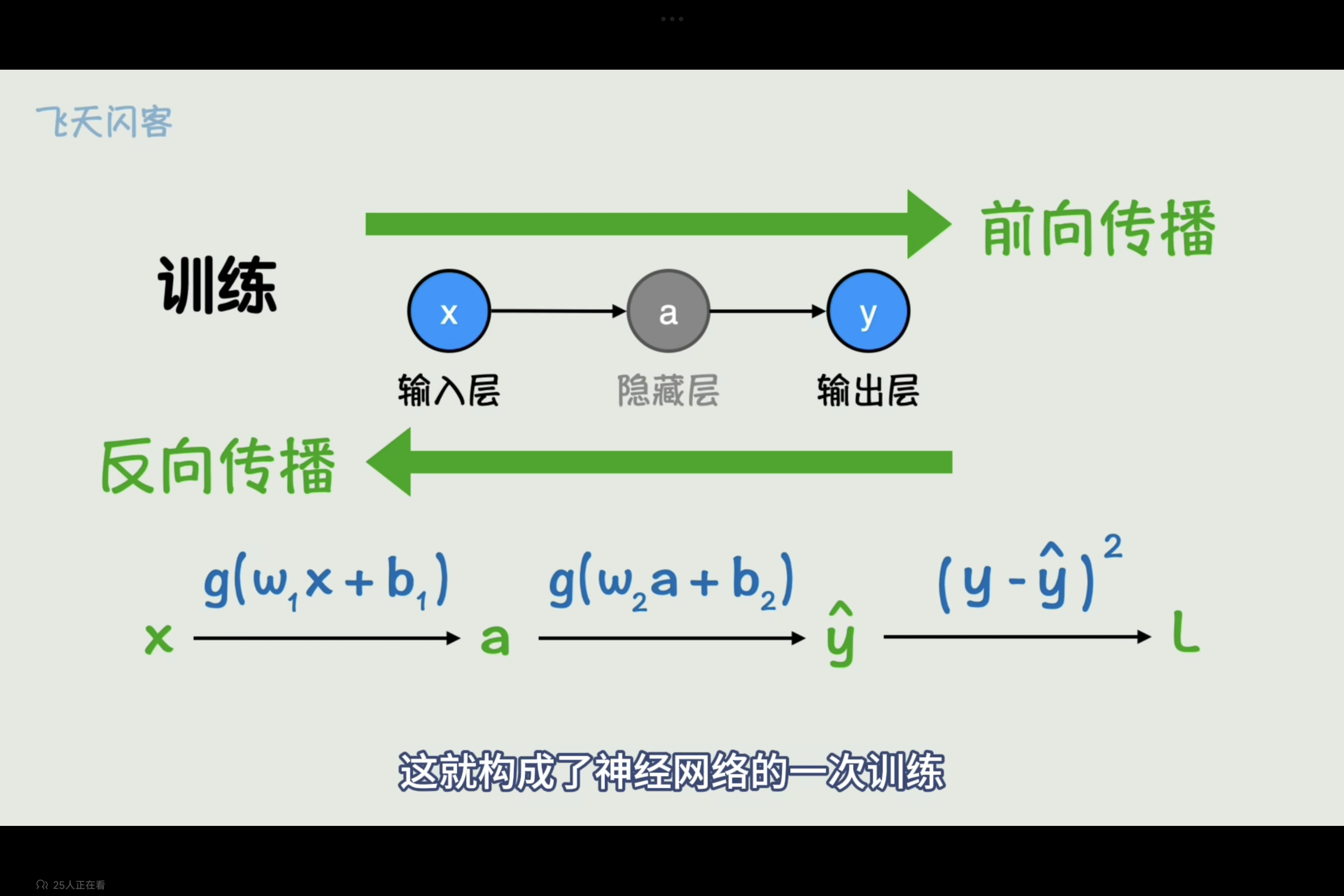
通过从输入x到输出y的前向传播，然后反向传播计算损失函数对每个参数的梯度，如果每个参数向着梯度反方向变化，构成神经网络一次训练。
过拟合
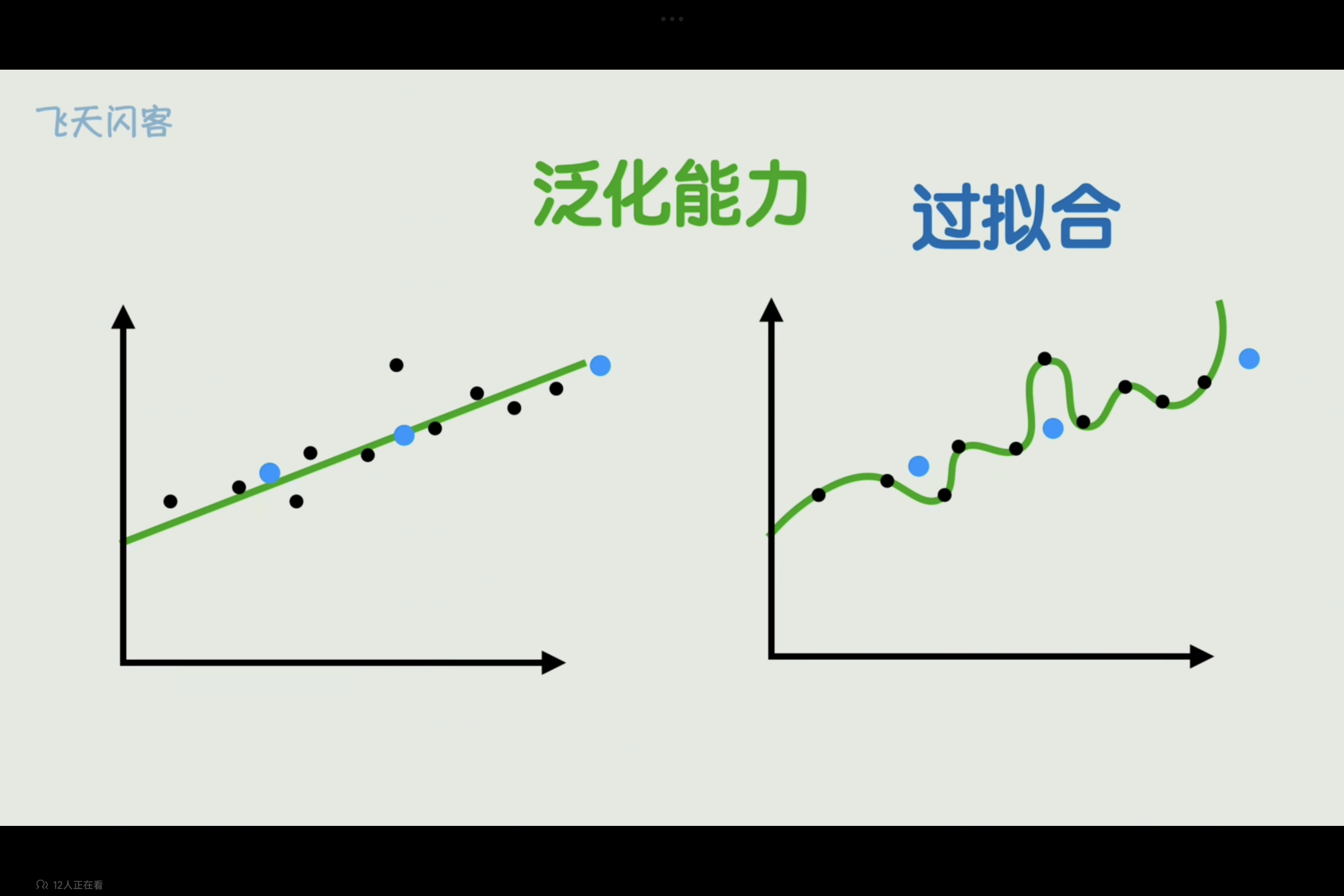
在训练数据上表现良好，对新数据预测泛化能力差的现象叫过拟合
模型学会了过于复杂的方法，以至于将噪声和随机波动一并考虑。
- 使用更多的数据量（数据增强：旋转，翻转，裁剪，噪声）
- 提前终止训练
- 修改损失函数添加惩罚项抑制参数过分增长（正则化：这种方法）
- Dropout：训练时丢弃部分参数防止对某些参数过度依赖
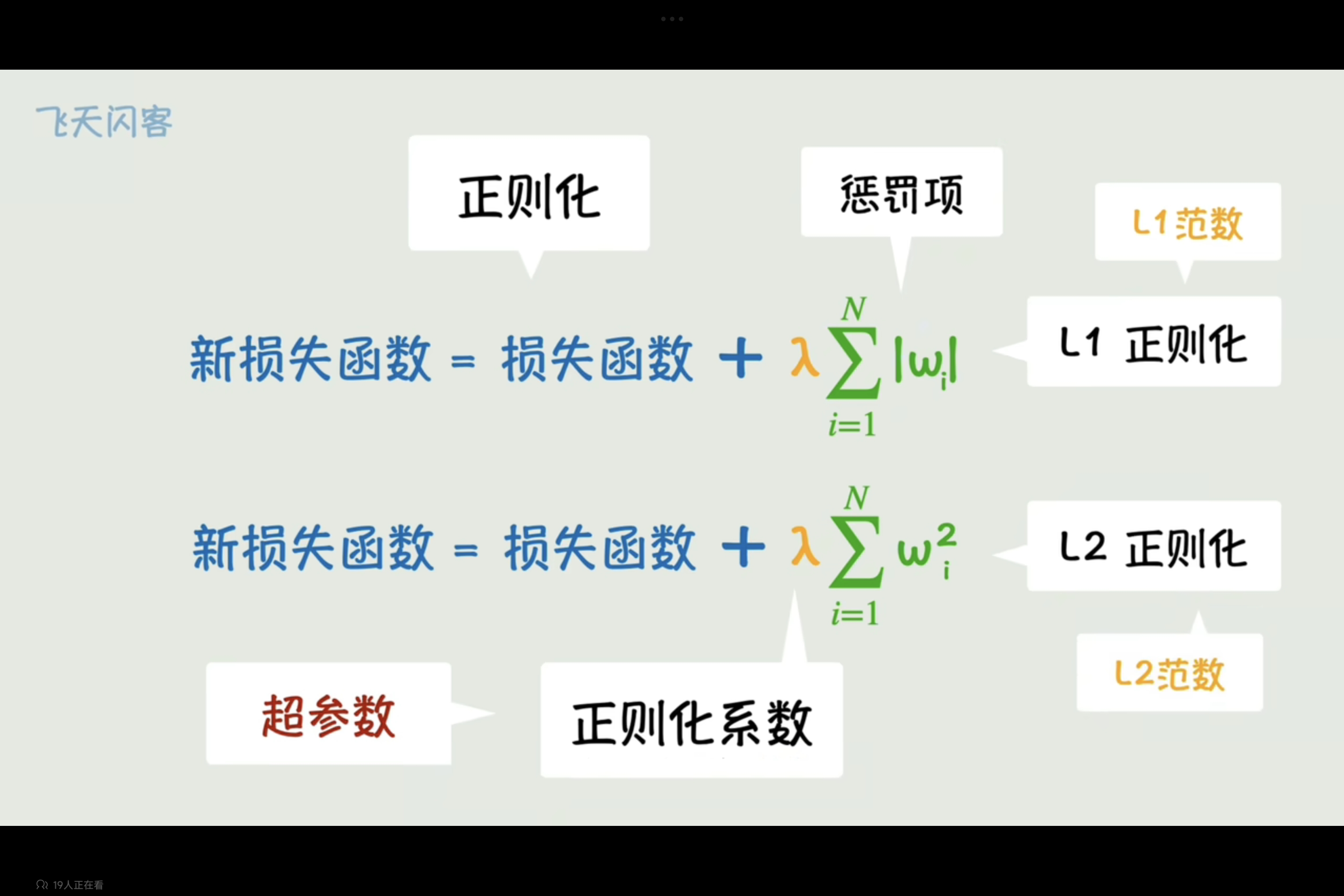
在损失函数中添加惩罚项，来抑制模型过分复杂，L1和L2，即惩罚项分别为参数绝对值和和参数平方和，L2在参数大时抑制效果更强。
控制惩罚力度的参数叫正则化系数，控制参数的参数叫超参数。
其他问题
- 梯度消失
- 梯度爆炸
- 收敛速度
- 计算开销
解决
- 梯度裁剪
- 残差网络Resnet
- Densenet
- 权重初始化
- 归一法
- 动量法
- RMSProp
- Adam
- mini-batch
矩阵
卷积
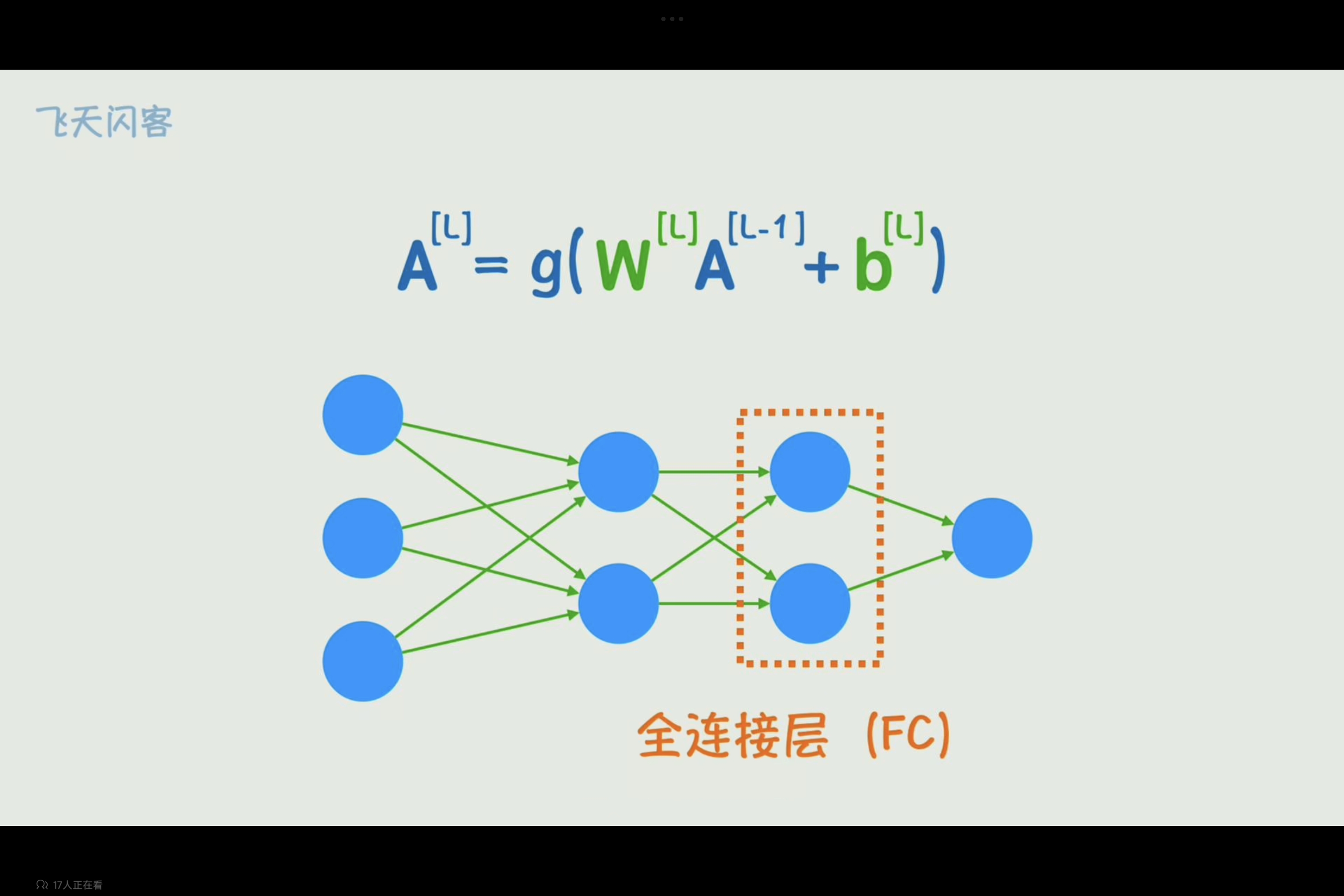
若要使用神经网络识别图片，按照像素平铺展开，例如，一个输入为 224x224x3 的图像，如果连接到一个有 1000 个神经元的全连接层，那么参数数量将非常庞大。则这个全连接层参数将超过百万级别，而且像素之间无法保留空间关系，会导致模型不能很好理解图像的局部模式。
卷积层通过卷积核在图像上滑动，并共享卷积核的权重。这意味着无论图像尺寸多大，卷积核的参数数量都是固定的。例如，一个 5x5 的卷积核，只有 25 个参数。
在传统的图像处理中，卷积操作使用一个预先定义好的、固定的矩阵（称为卷积核、滤波器或掩码）在图像上滑动。这个矩阵中的数值决定了卷积操作的行为。
- 模糊: 使用平均滤波器或高斯滤波器。
- 锐化: 使用拉普拉斯算子或Sobel算子。
- 边缘检测: 使用Sobel算子、Prewitt算子或Canny算子。
- 浮雕: 使用特定的矩阵来模拟光照效果。
卷积操作实际上是计算卷积核与图像局部区域的加权和。通过改变卷积核中的权重，可以突出或抑制图像中的某些特征，从而达到图像处理的目的。
卷积神经网络（Convolutional Neural Network，CNN）
卷积层（Convolution Layer）
在卷积神经网络中，与传统的图像处理不同，CNN（卷积神经网络）中的卷积核不是预先定义的，而是通过机器学习（通常是反向传播算法）从大量数据中学习得到的。CNN 通过训练，不断调整卷积核中的数值，使其能够更好地识别和提取图像中的特征，从而提高图像识别、分类或其他任务的准确性。
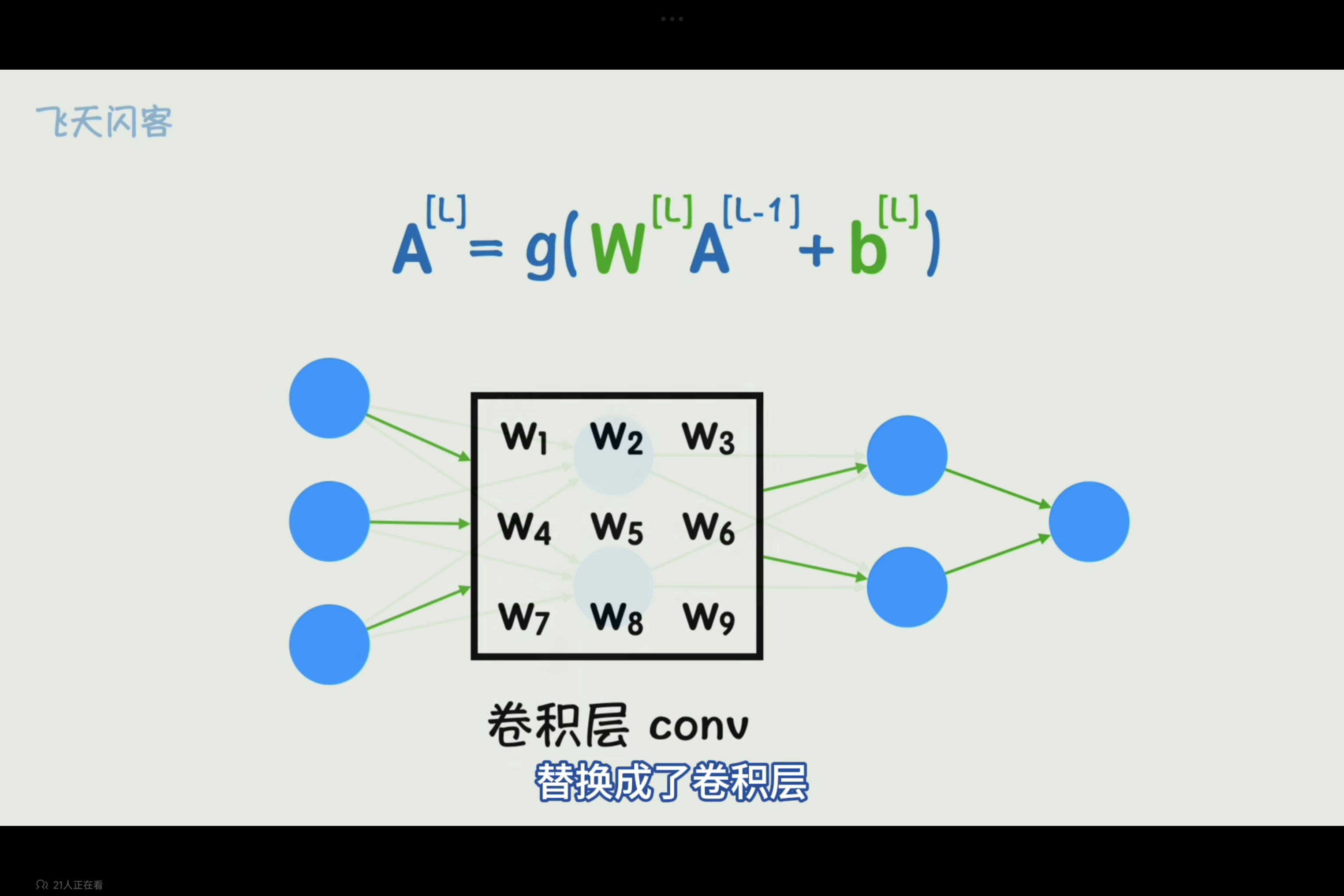
卷积层可以替换神经网络中一层全连接层，起到减少权重参数，有效提取局部特征的作用
池化层（Pooling Layer）
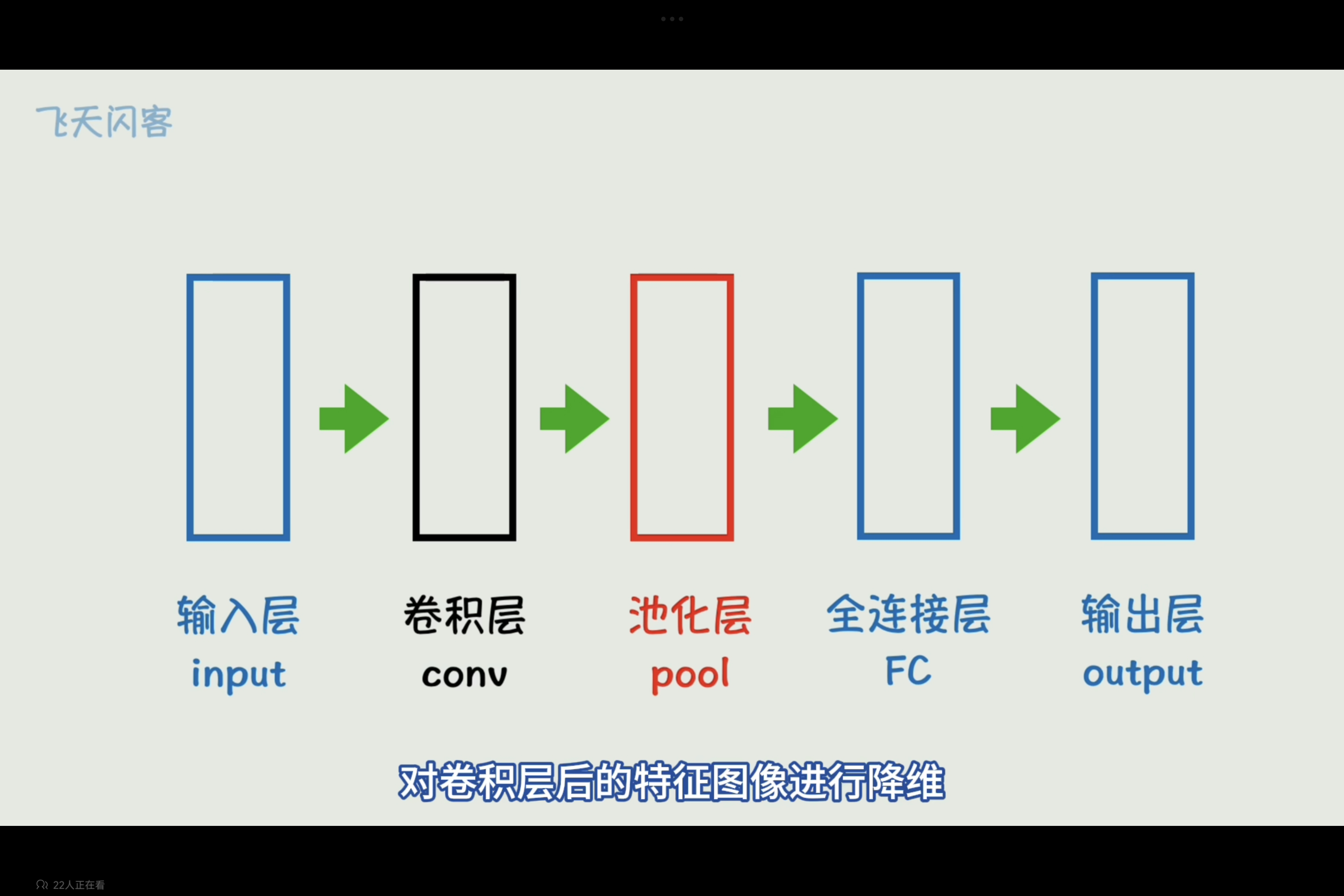
与卷积层配合使用的一般还有池化层（Pooling Layer），池化层起到的作用是在保留重要特征的同时，降低特征图的空间维度，从而减少计算量和参数数量。
循环神经网络（Rerrent Neural Network, RNN）
词嵌入（word embedding）
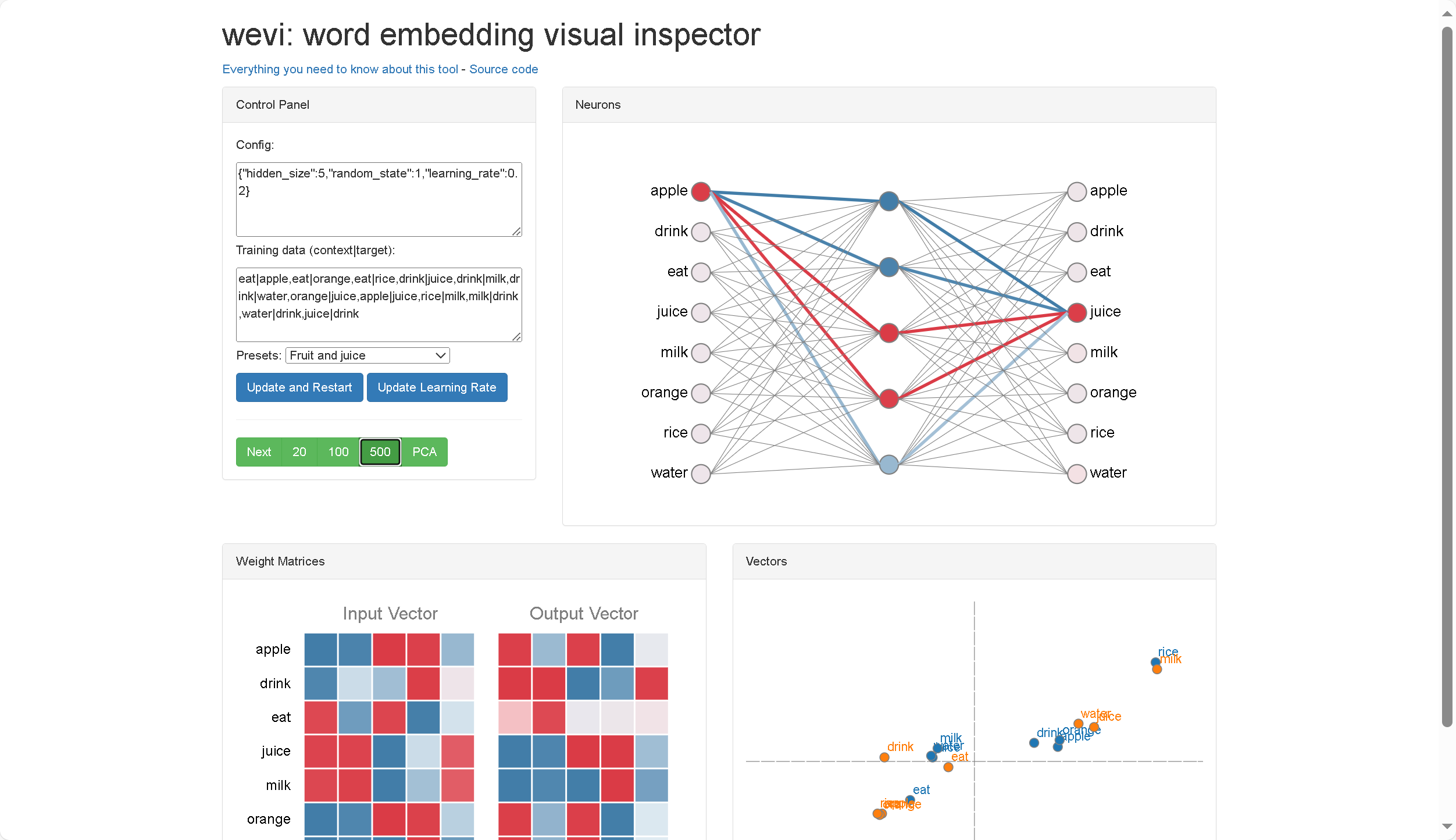
词嵌入（Word Embedding）是一种将自然语言中的词语映射到低维向量空间的技术。简单来说，就是把每个词都变成一个向量，这个向量能够捕捉到词语的语义信息，使得语义相似的词在向量空间中距离更近。
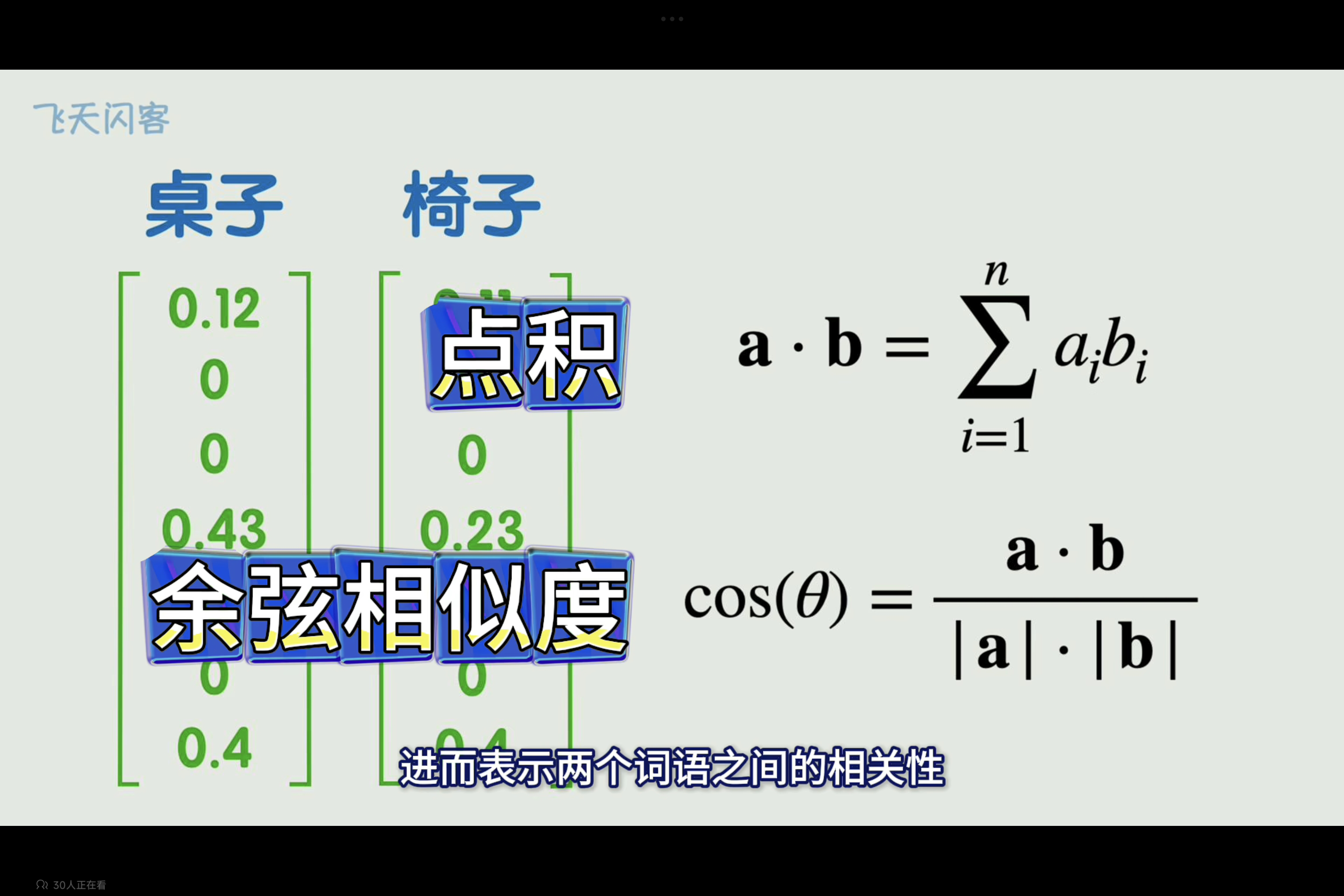
通过计算两个词向量的点积或者余弦相似度，可以表示向量之间的相关性。
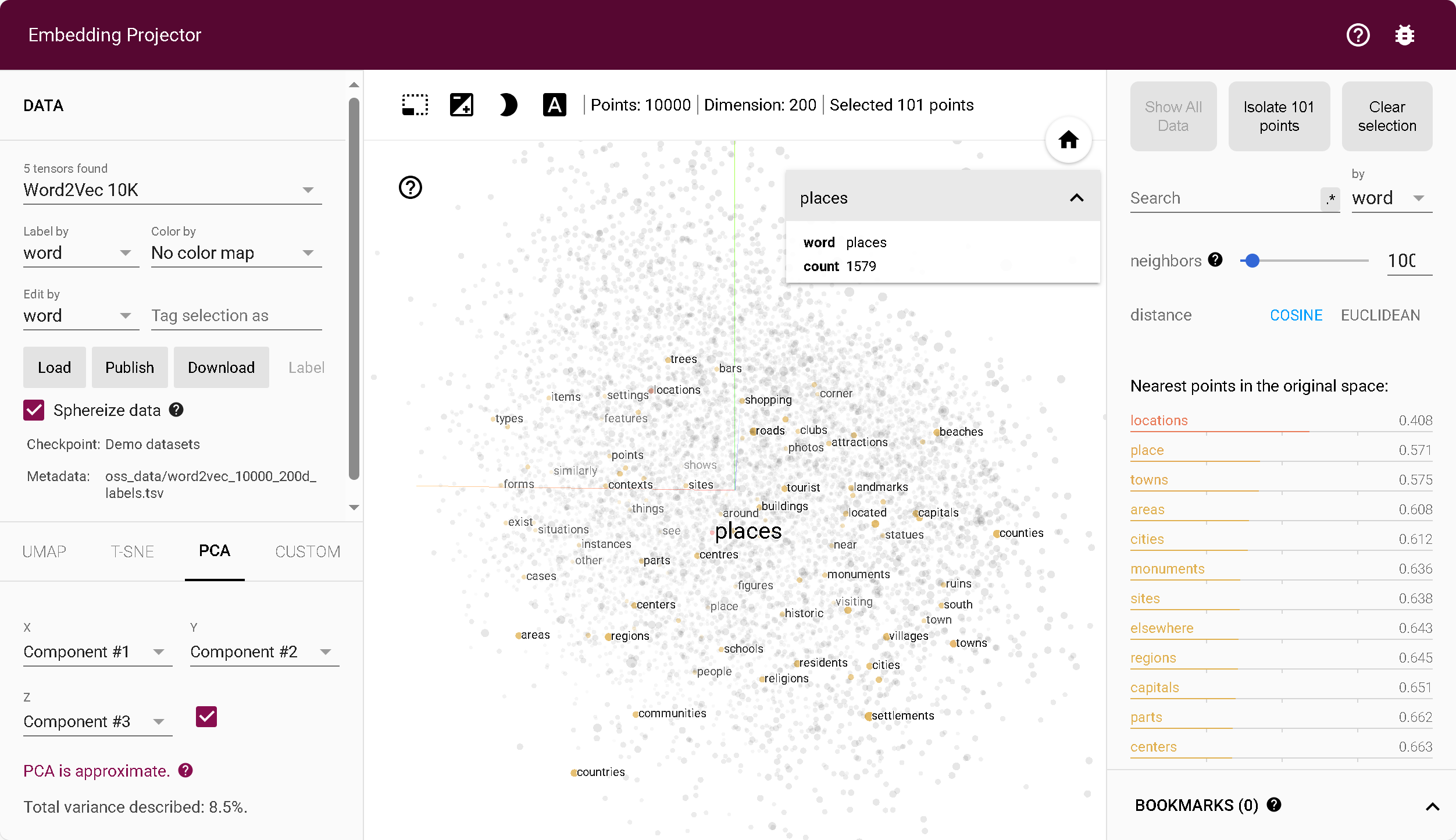
词向量嵌入矩阵潜空间降维投影到坐标系，可视化不同词语之间的距离
Embedding projector - visualization of high-dimensional data
为了将上一词的词义与后文产生联系，可以将第一词的隐藏状态和第二词一起参数运算，依次传递，就可使得后文具有前词的信息。
既是RNN循环神经网络，是一种专门用于处理序列数据的神经网络。与传统的前馈神经网络不同，RNN 具有循环连接，使得它可以将之前的状态信息传递到当前状态，从而能够处理具有时序关系的序列数据。
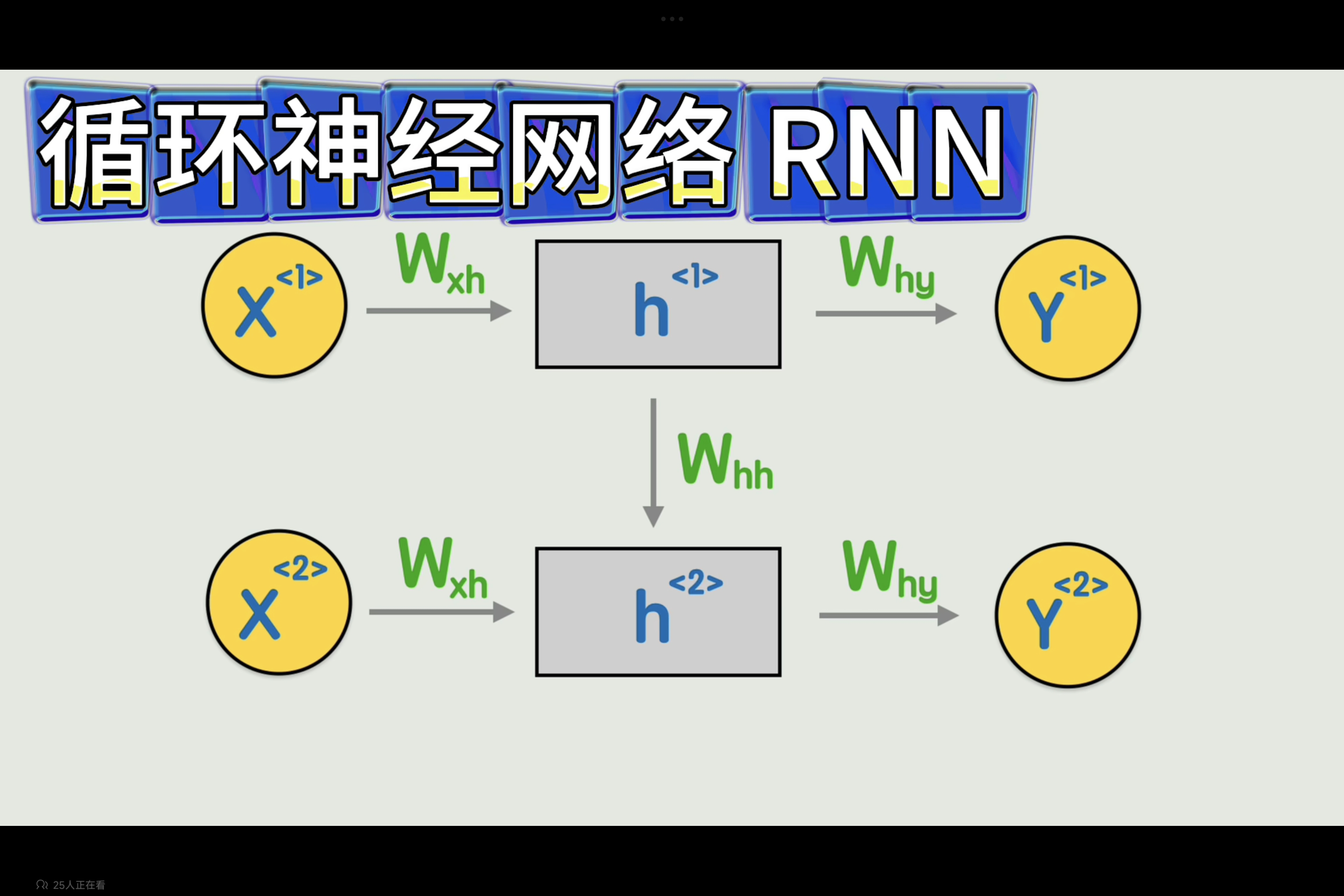
详细流程如下：
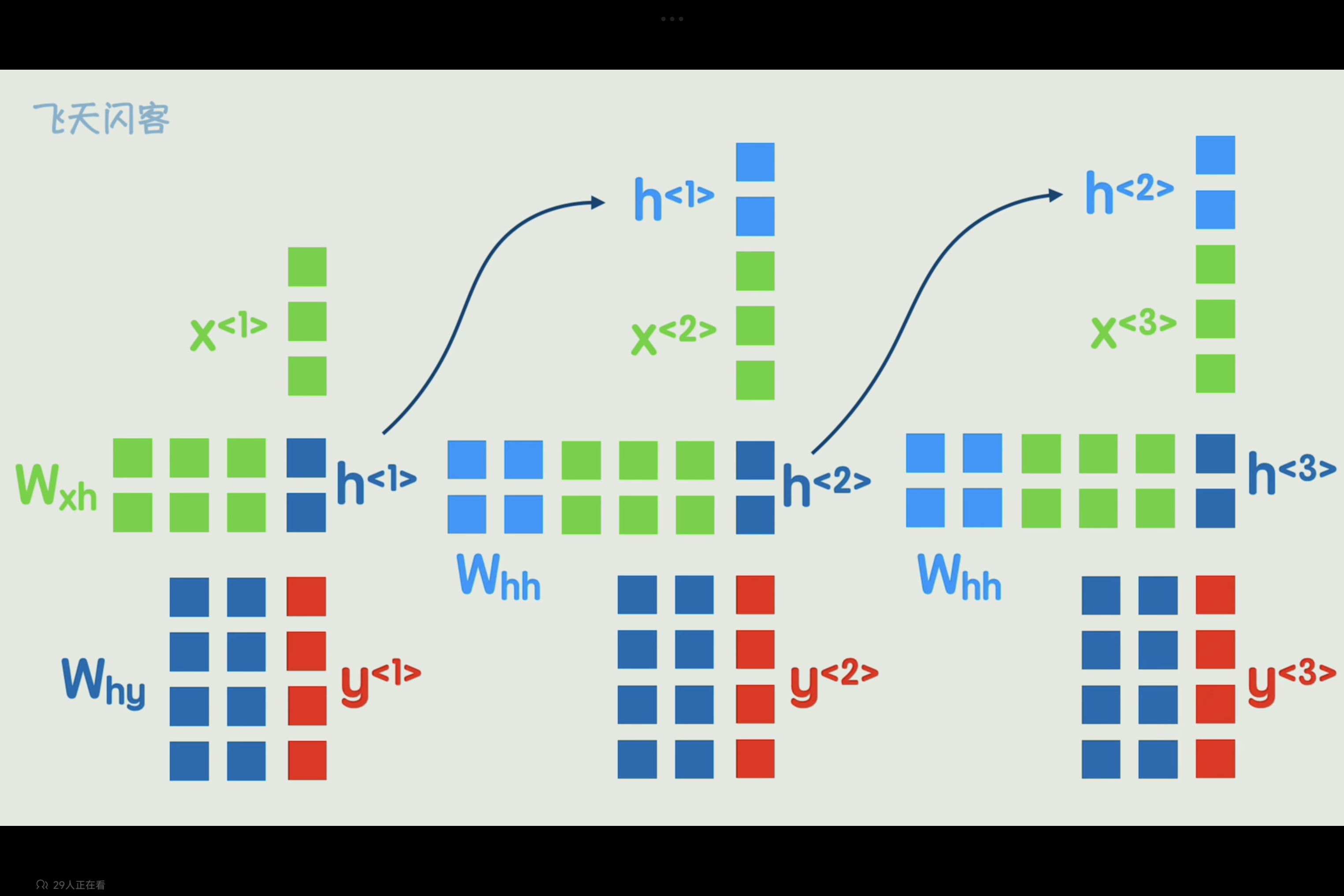
和经典神经网络相比，仅仅是多了一个前一时刻的隐藏状态。
Transformer
Transformer 是一种基于自注意力机制（Self-Attention Mechanism）的神经网络架构，最初由 Google 在 2017 年的论文 “Attention is All You Need” 中提出。它彻底改变了自然语言处理（NLP）领域，并在机器翻译、文本生成、问答系统等任务中取得了显著的成果。
wechat
Alipay
