机器学习——深度学习

机器学习

机器学习是一个专门研究和开发能够学习的机器的领域，目标是获得通用人工智能。

机器学习是人工智能的核心领域，目标是让计算机通过数据学习规律并做出预测或决策。其核心逻辑是：从数据中提取特征，通过算法训练模型，实现对未知数据的推断。

• 分类：包括监督学习（如回归、分类算法）、无监督学习（如聚类、降维）、半监督学习和强化学习等。
• 关键特征：依赖人工设计的特征工程，例如在图像识别中，需要手动提取边缘、颜色等特征。

本篇是对之前文章的扩展，补充与深化，本人深感过去文章水平有限，仅是为完成工程任务调参了解的，极为片面，浅薄的记录，本文试图作为学习笔记系统性记录✍️本人的学习过程。(ﾉ∇︎〃 )

添加了很多骚话个人理解(´つヮ⊂︎)

前面大多为车轱辘话(╯‵□′)╯︵┻━┻，只需要大致了解概念。可直接跳至算法原理。(ฅ>ω<*ฅ)

序言

一些很漂亮很浪漫很有人类探索精神的屁话╮(╯▽╰)╭

千百年来，人类试图了解智能的机制，并将它复制到思维机器上。

人类从不满足于让机械或电子设备帮助做一些简单的任务，例如，使
用燧石打火，使用滑轮吊起沉重的岩石，使用计算器做算术。

相反，我们希望能够自动化执行更具有挑战性、相对复杂的任务，如
对相似的照片进行分组、从健康细胞中识别出病变细胞，甚至是来一盘优雅的国际象棋博弈。这些任务似乎需要人类的智能才能完成，或至少需要人类思维中的某种更深层次、更神秘的能力来完成，而在诸如计算器这样简单的机器中是找不到这种能力的。
具有类似人类智能的机器是一个如此诱人且强大的想法，我们的文化
对它充满了幻想和恐惧，如斯坦利·库布里克导演的《2001: A Space
Odyssey》中的HAL 9000（拥有巨大的能力却最终给人类带来了威胁）、动作片中疯狂的“终结者（Terminator）”机器人以及电视剧《Knight Rider》中具有冷静个性的话匣子KITT汽车。

1997年，国际象棋卫冕世界冠军、国际象棋特级大师加里·卡斯帕罗夫
被IBM“深蓝”计算机击败，我们在庆祝这一历史性成就的同时，也担心机
器智能的潜力。

神经网络

机器学习－－神经网络

之前在学习Nanodet模型时，对于神经网络非常浅显的记录

计算机可以以相当快的速度在短时间内执行数亿次数学运算，能够高效的数量海量数据，但是在很长一段时间内，计算机却无法做到人类能够轻易完成的任务，仅通过视觉以极快的速度识别身边的物体，无意识间控制四肢协调平衡运动，等等。

而我们却能够仅仅为大脑提供大概20w的功耗轻易做到复杂的计算机无法完成的任务。不禁让很多人试图再次利用仿生学在计算机上实习以上功能。

依旧骚话✧(◍˃̶ᗜ˂̶◍)✩

最早的神经网络模型–感知机

那就回到1957年，找到美国心理学家弗兰克·罗森布拉特（Frank Rosenblatt），一个神经生物学和行为学副教授，提出一种单层神经网络模型，旨在模拟生物神经元工作原理，由输入层，隐藏层，和输出层组成。

其非常简单，输入问题，进行计算，得到结果，如果存在差异则更新内部权重，这即是训练过程。

你可能会想“这也没什么了不起的吧！”，这确实没什么了不起╮(╯▽╰)╭，你是这样想的，我也是。但这是由于当时技术的局限和理论的不完善，其确实是神经网络历史上最早提出的模型之一，也是现代深度学习的先驱，为后来的多层感知机和深度学习模型提供了理论支持，开创了人工神经网络的研究。

神经网络

虽然神经元有各种形式，但是所有的神经元都是将电信号从一端传输到另一端，沿着轴突，将电信号从树突传到树突。然后，这些信号从一个神经元传递到另一个神经元。这就是身体感知光、声、触压、热等信号的机制。来自专门的感觉神经元的信号沿着神经系统，传输到大脑，而大脑本身主要也是由神经元构成的。

我们需要多少个神经元才能执行相对复杂的有趣任务呢？

一般说来，能力非常强的人类大脑有大约1000亿个神经元！一只果蝇
拥有约10万个神经元，能够飞翔、觅食、躲避危险、寻找食物以及执行许多相当复杂的任务。10万个神经元，这个数字恰好落在了现代计算机试图复制的范围内。一只线虫仅仅具有302个神经元，与今天的数字计算机资源相比，简直就是微乎其微！但是一只线虫能够完成一些相当有用的任务，而这任务对于尺寸大得多的传统计算机程序而言却难以完成。

激活函数

观察表明，神经元不会立即反应，而是会抑制输入，直到输入增强，
强大到可以触发输出。你可以这样认为，在产生输出之前，输入必须到达一个阈值。就像水在杯中——直到水装满了杯子，才可能溢出。直观上，这是有道理的——神经元不希望传递微小的噪声信号，而只是传递有意识的明显信号。下图说明了这种思想，只有输入超过了阈值（threshold），足够接通电路，才会产生输出信号。

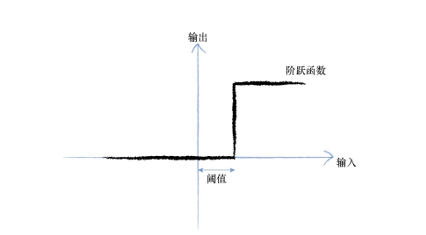
我们可以改进阶跃函数。下图所示的S形函数称为S函数（sigmoid function）。这个函数，比起冷冰冰、硬邦邦的阶跃函数要相对平滑，这使 得这个函数更自然、更接近现实。

$$
f(x) = \frac{1}{1 + e^{-x}}
$$

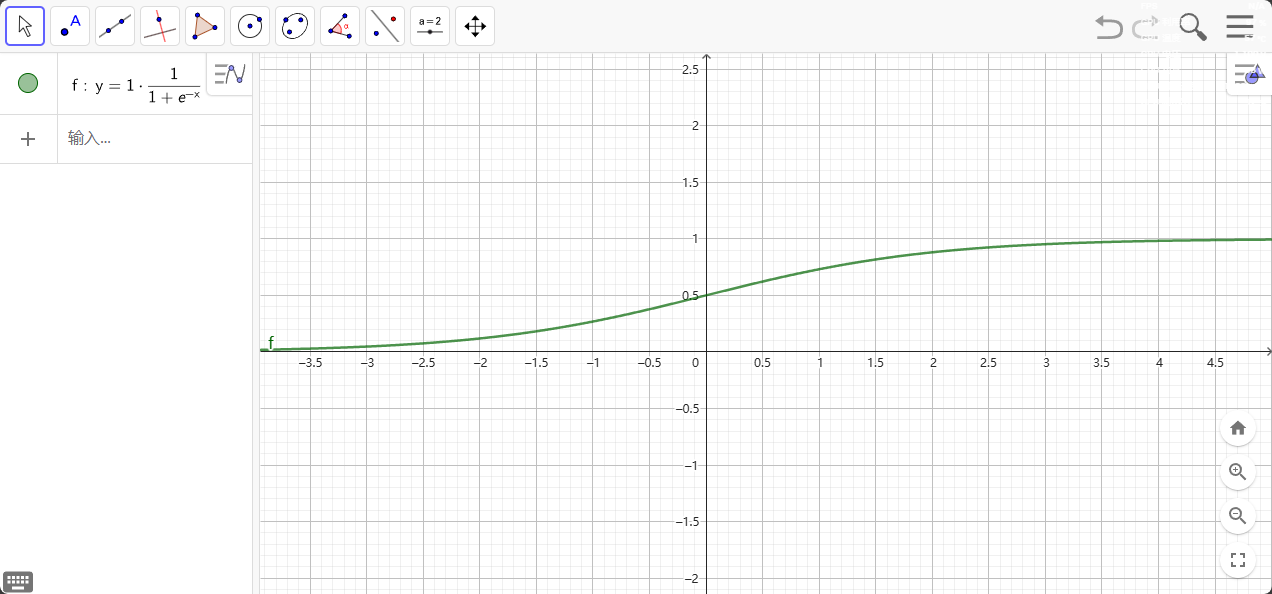
随着输入 x 的增加，sigmoid 函数的输出会接近 1，但永远不会达到 1。同样，当输入值减小时，S 型函数值 函数的输出接近，但永远不会达到 0。

sigmoid 一词通常更广泛地用于指代任何 S 形函数。从技术层面来看，对特定函数$f(x) = \frac{1}{1 + e^{-x}}$来说，更准确的术语是逻辑函数。

sigmoid function是机器学习中重要的激活函数

• Sigmoid函数的输出范围是0到1。由于输出值限定在0到1，因此它对每个神经元的输出进行了归一化。
• 用于将预测概率作为输出的模型。由于概率的取值范围是0到1，因此Sigmoid函数非常合适
• 梯度平滑，避免跳跃的输出值
• 函数是可微的。这意味着可以找到任意两个点的Sigmoid曲线的斜率
• 结果明确，即非常接近1或0。
• 函数输出不是以0为中心的，这会降低权重更新的效率
• Sigmoid函数执行指数运算，计算机运行得较慢。

sigmoid激活函数在神经网络中起到的作用：

引入非线性特性，神经网络基本单元是线性组合（加权求和），部分情况需要映射到非线性解决复杂情况$f(x) = \frac{1}{1 + e^{-x}}$

sigmoid通常用于二分类最后一层，输出结果在0-1之间，将结果解释为“某一类的概率”

反向传播便利性 ，因为sigmoid函数可导，复合求导可得$\sigma’(x) = \frac{1}{1+e^{-x}} \cdot \frac{e^{-x}}{1+e{-x}} = \sigma(x)(1-\sigma(x))$便于反向传播中梯度计算

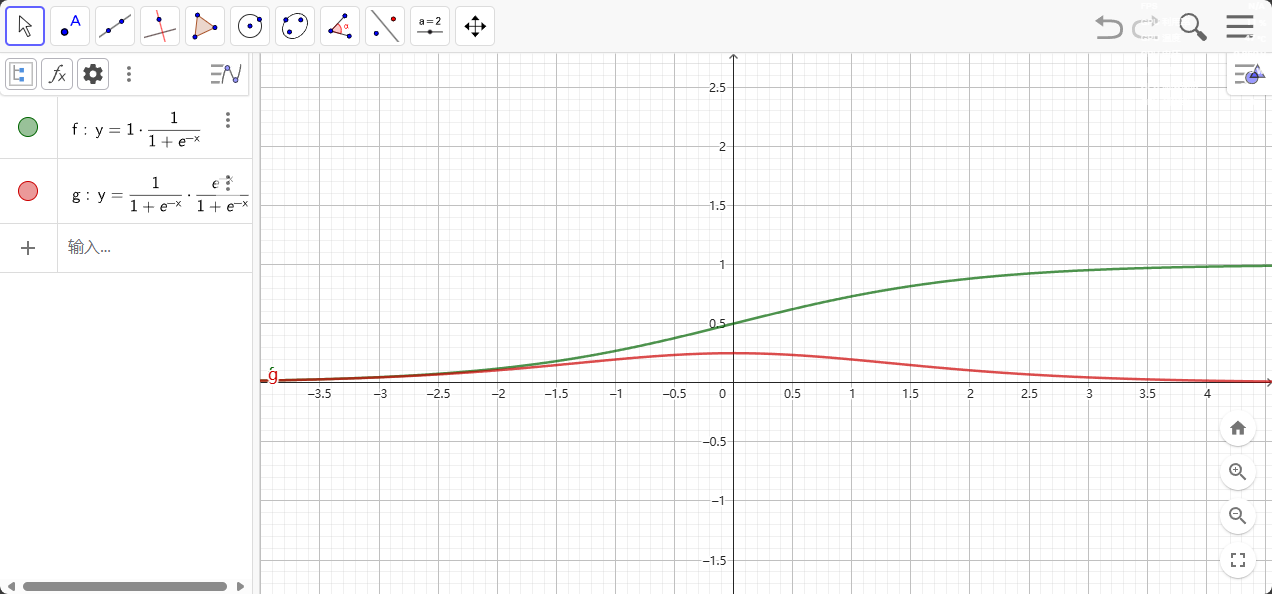
其他激活函数

双曲正切激活函数

$$
F(x)=tanh(x)
$$

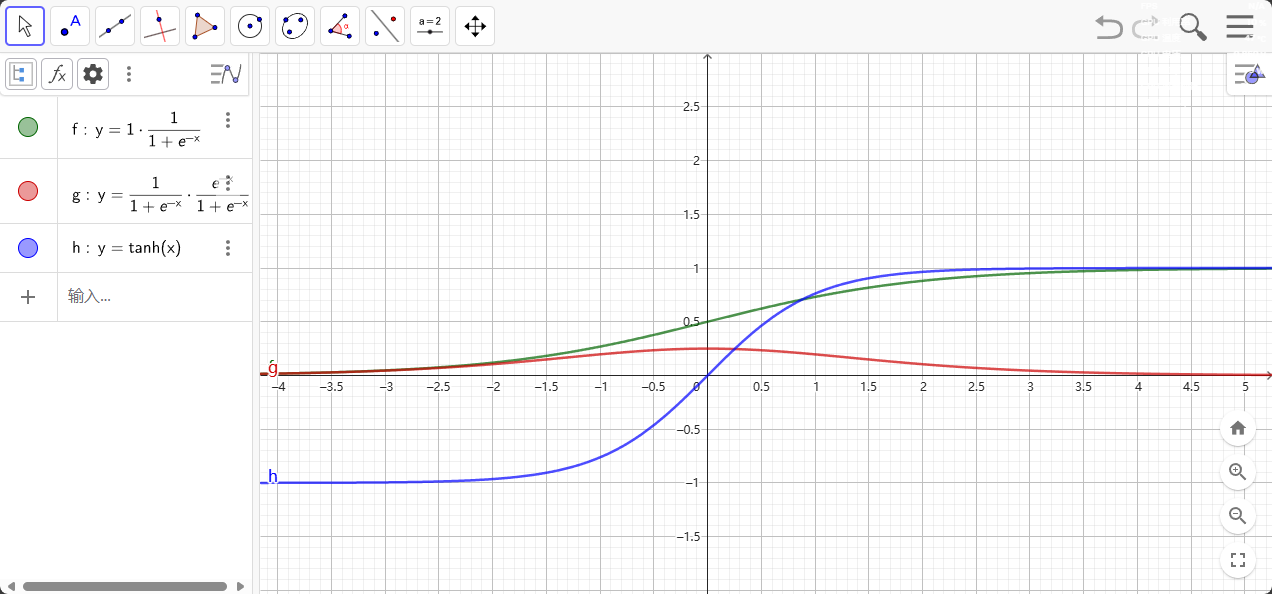
请注意，S 型函数的范围为 0 到 1，tanh 函数的范围为 -1 到 1

修正线性单元激活函数（简称 ReLU）

$$
F(x)=max(0,x)
$$

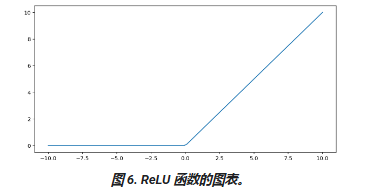
ReLU 作为激活函数的效果通常优于 S 型函数或 tanh 等平滑函数，因为它在神经网络训练期间不易受到梯度消失问题的影响。与这些函数相比，ReLU 的计算也更容易。

矩阵

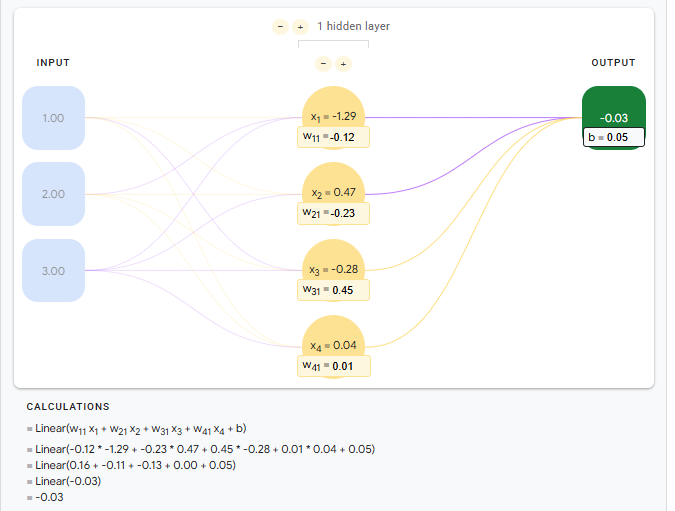
下面是一个简单的全连接层

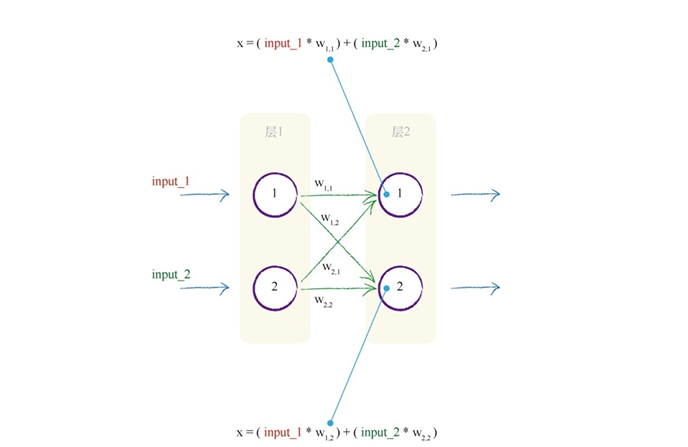
对于第二层，二层一同时接受一层一和一层二的输出，对于此处简单的计算，我们可以得到$X=(input1w_{1,1})+(input2w_{2,1})$,但是实际上的全连接层需要计算的连接个数众多，使用这种计算方法即不直观，而且串行运算在计算机中运行时消耗许多内存交换以及等待时间，显然，我们需要矩阵运算。

对于第二层神经元接受到的信号强度可以使用$X=W•I$计算，W是权重矩阵，I是输入矩阵，X 是输入到第二层的结果矩阵。

$$X=\left[\begin{array}{cc}{w}_{1,1}& w_{2,1}\\ w_{1,2}& w_{2,2}\end{array}\right]\left[\begin{array}{c}input1\\ input2\end{array}\right]=\left[\begin{array}{c}(input1\ast w_{1,1}+input2\ast w_{2,1})\\ (input1\ast w_{1,2}+input2\ast w_{2,2})\end{array}\right]$$

使用矩阵可以清晰描述，并且能够直接计算一层权重。

隐藏层

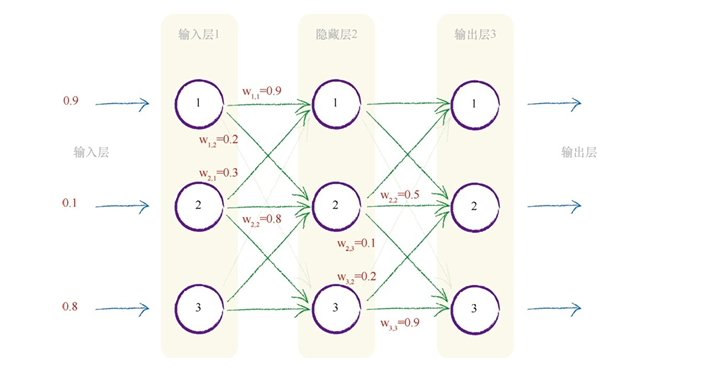
隐藏层，位于神经网络中间层，即既不作为输入也不作为输出，在中间起连接，传递作用的。

$W_{input_hidden}$是输入层和隐藏层之间的权重,$W_{hidden_output}$是隐藏层和输出层之间的权重

$$
X_{hidden}=W_{input_hidden}•Input
$$

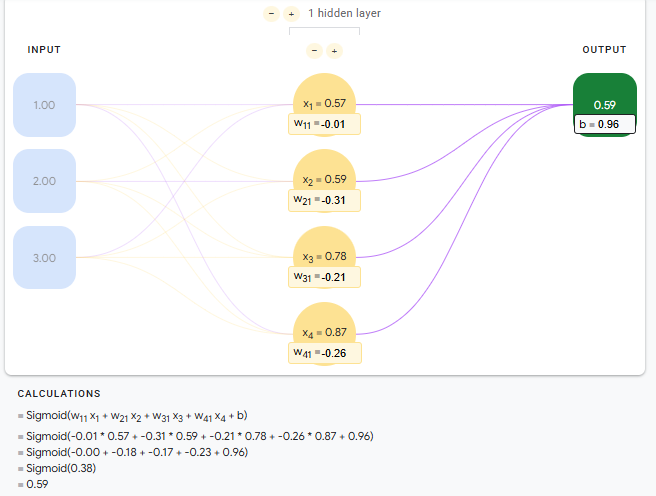
隐藏层的输出可以再使用激活函数。

$$
Output_{hidden} = sigmoid(X_{hidden})
$$

计算输出层权重

$$
X_{output}=W_{hidden_output}•Output_{hidden}
$$

使用激活函数

$$
Output_{output}=sigmoid(X_{output})
$$

神经单元线性关系

神经单元使用激活函数非线性关系

神经网络（Neural Network，NN）是机器学习中的一种算法框架，灵感源于生物神经元，通过多层节点（神经元）连接传递信息，实现复杂映射。

• 结构：由输入层、隐藏层、输出层组成，层间神经元通过权重连接，通过反向传播算法优化权重。
• 典型模型：早期的感知机、多层感知机（MLP），但受限于计算能力和数据量，应用范围较窄。

深度学习

深度学习（Deep Learning）本质上是多层神经网络的深化，通过增加网络层数（如几十层到上千层）和复杂结构，实现对数据的自动特征提取和表示学习。

深度学习是神经网络的延伸与升级，计算能力的提升解决了传统神经网络训练算力问题，使得深度学习具有更为复杂的结构，能够实现更为复杂的功能。

• 自动特征工程：无需人工设计特征，例如CNN可自动提取图像的边缘、纹理等高层特征，RNN可处理序列数据的时序关系。

卷积神经网络（CNN）、循环神经网络（RNN）、Transformer、生成对抗网络（GAN）等，广泛应用于图像识别、自然语言处理、语音识别等领域。

什么是机器学习

使计算机不需要显式编程就能拥有学习能力的研究

机器通过观察某项任务存在的模式，并且试图以某种直接或间接方式模仿。

而直接或间接的区别即分为监督学习和非监督学习

监督学习

• 数据特点：输入数据（特征）配有明确的标签（Label），即“有标准答案”。
• 示例：图像分类任务中，每张图片标注“猫”“狗”等类别；房价预测中，房屋特征（面积、位置）对应具体价格。
• 如线性回归，决策树，SVM，CNN

非监督学习

• 数据特点：输入数据无标签，仅包含特征，需算法自行发现数据内在结构。
• 示例：用户行为数据（浏览记录、购买偏好）未标注类别，需通过聚类算法将相似用户分组。
• 如k-means，PCA，AE

监督学习

• 本质：通过“输入特征+标签”的标注数据，学习从特征到标签的映射关系（函数），再用训练好的模型对新数据预测。
• 类比理解：类似学生通过“例题（标注数据）”学习解题规则，再用规则解答新题目。

1.数据要求

• 必须包含特征（Features） 和标签（Labels），如：
• 图像分类：像素值是特征，“猫/狗”是标签；
• 房价预测：房屋面积、位置是特征，价格是标签。

2.学习目标

• 最小化预测值与真实标签的误差，例如：
• 用线性回归预测房价时，让模型输出的价格与实际价格尽可能接近。

3. 训练流程：

• 划分训练集、验证集和测试集 → 模型拟合训练数据 → 通过验证集调参 → 用测试集评估泛化能力。

无监督学习

• 本质：仅通过输入特征（无标签），让模型自主发现数据的内在规律（如相似性、聚类结构、分布模式）。
• 类比理解：类似人类在没有老师指导的情况下，通过观察事物特征（如颜色、形状）自主将其分组（如将水果按大小、甜度分类）。

主要是聚类和降维

聚类（Clustering）：数据分组

• 目标：将相似的数据点归为同一簇（Cluster），不同簇间差异明显。
• 示例：
• 电商平台根据用户购买行为（浏览记录、消费金额）将用户分群，针对性推送商品；
• 生物学中按基因表达数据对物种分类。

降维（Dimensionality Reduction）：特征压缩

• 目标：将高维数据（如上万维特征）映射到低维空间，保留关键信息，减少计算复杂度。

参数学习和非参数学习

机器学习可以分为有无监督，也可分为有无参数

参数学习，即数据服从某种固定分布，通过训练数据学习一组固定数量的参数，用固定参数直接描述数据模型。

非参数学习，即不预设参数数量，依赖数据本身，模型复杂度会随之动态变化。

参数学习：典型算法与原理

1. 线性回归（Linear Regression）

• 核心：假设输出与输入是线性关系，用参数 \theta 表示权重，通过最小化均方误差（MSE）求解 \theta 。
• 公式： $y = \theta_0 + \theta_1x_1 + \dots + \theta_nx_n $，参数数量为特征维度+1（固定）。

2. 逻辑回归（Logistic Regression）

• 核心：在线性回归基础上用Sigmoid函数将输出映射到[0,1]区间，用于二分类，参数含义与线性回归类似。
• 应用：垃圾邮件分类、疾病预测（是否患病）。

3. 朴素贝叶斯（Naive Bayes）

• 核心：假设特征条件独立，学习先验概率 P(Y) 和条件概率 P(X|Y) （如高斯朴素贝叶斯假设 P(X|Y) 服从高斯分布）。
• 参数：存储各类别概率和特征分布参数（如均值、方差），数量固定。

非参数学习：典型算法与原理

1. K近邻（K-Nearest Neighbors, KNN）

• 核心：不学习参数，直接存储所有训练样本。预测时找新样本的K个最近邻，根据邻居类别投票（分类）或取均值（回归）。
• 特点：
• 无固定参数，K是超参数（需手动调优），模型复杂度随样本量增加而提高；
• 适合处理图像像素级分类（如MNIST手写数字识别）。

2. 决策树（Decision Tree）

• 核心：通过递归划分特征空间（如按“年龄>30岁”“收入>5000元”等条件分裂节点），树的深度和节点数由数据决定（非固定参数）。
• 变种：随机森林（集成多棵决策树，非参数特性更强）。

3. 核密度估计（Kernel Density Estimation, KDE）

• 核心：不假设数据分布，用核函数（如高斯核）平滑每个数据点的概率密度，整体密度由所有点叠加而成。
• 应用：估计数据的概率分布（如金融市场收益率的分布预测）。

4. 支持向量机（SVM，非参数视角）

• 核心：当使用非线性核函数（如RBF核）时，SVM通过将数据映射到高维空间求解分隔超平面，模型复杂度与支持向量数量相关（数据量越大，支持向量可能越多）。